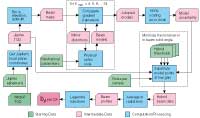
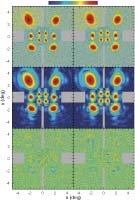
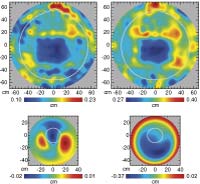
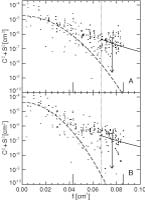
Beam Maps and Window Functions
Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Beam Maps and Window Functions, R. Hill, et al., 2009ApJS..180..246H, reprint / preprint (1.4 MB) / bundled figures (995 KB) / individual figures / ADS / astro-ph
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||