For model 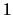 , the probability distribution for the number
, the probability distribution for the number 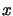 of
electrons generated by impact ionisation from a gain stage when one
electron is input is defined by a Poisson distribution:
of
electrons generated by impact ionisation from a gain stage when one
electron is input is defined by a Poisson distribution:
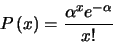 |
(4.1) |
where
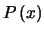 is the probability distribution for the
number
is the probability distribution for the
number 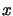 of additional charge carriers generated and
of additional charge carriers generated and 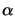 is the
expectation value for the number of additional charge carriers
generated. The variance of the Poisson distribution is equal to the
expectation value
is the
expectation value for the number of additional charge carriers
generated. The variance of the Poisson distribution is equal to the
expectation value 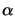 .
.
It is perhaps more useful to describe
Equation 4.1 in terms of the total number
of output electrons 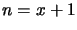 (i.e. including the single input
electron):
(i.e. including the single input
electron):
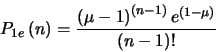 |
(4.2) |
where
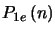 is the probability distribution for
the total number of output electrons and
is the probability distribution for
the total number of output electrons and 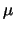 is the expectation
value for the total number of output electrons (equal to the gain of
the stage;
is the expectation
value for the total number of output electrons (equal to the gain of
the stage; 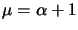 ). As the charge transfer efficiency is
perfect,
). As the charge transfer efficiency is
perfect, 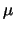 is always greater than or equal to one. The variance in
the total number of output electrons is equal to the gain minus one:
is always greater than or equal to one. The variance in
the total number of output electrons is equal to the gain minus one:
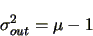 |
(4.3) |
As the model is linear and the electrons are treated independently,
the variance in the number of output electrons for a fixed number of
input electrons 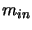 is just:
is just:
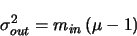 |
(4.4) |
If there is a variance
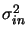 in the number
in the number
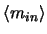 of input electrons, the total variance in the number of
output electrons
of input electrons, the total variance in the number of
output electrons
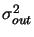 is just:
is just:
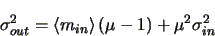 |
(4.5) |
Bob Tubbs
2003-11-14
![]() (i.e. including the single input
electron):
(i.e. including the single input
electron):
![]() in the number
in the number
![]() of input electrons, the total variance in the number of
output electrons
of input electrons, the total variance in the number of
output electrons
![]() is just:
is just: