Next: Calculating the probability distribution Up: Simple models of the Previous: Statistical properties of registers Contents
If the multiplication register is enabled, then the expectation value for the number of output electrons will be increased by a factor equal to the total multiplication register gain. The variance in the number of output electrons will also be increased, as described by Equations 4.11 and 4.12 for models 1 and 2 respectively. If the output of the multiplication register is treated in an analogue fashion (in the same way as for a conventional CCD), then this variance acts as a source of additional noise.
The signal-to-noise ratio for a register containing ![]() stages each giving a
gain of
stages each giving a
gain of ![]() is:
is:
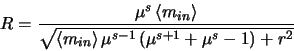 |
(4.15) |
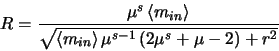 |
(4.16) |
For large multiplication register gains (
![]() ) the readout noise of the CCD becomes negligible giving:
) the readout noise of the CCD becomes negligible giving:
It is interesting to compare the signal-to-noise in
Equation 4.20 with the signal-to-noise ![]() for an ideal readout-noise free detector (limited only by photon shot
noise):
for an ideal readout-noise free detector (limited only by photon shot
noise):
| (4.21) |
In an ideal readout-noise free detector a reduction by a factor of
![]() in signal-to-noise would be brought about if the quantum
efficiency of the detector was halved. The noise performance of the
L3Vision devices is thus similar to the performance of a readout-noise
free device with half the quantum efficiency (see also
Mackay et al. (2001)).
in signal-to-noise would be brought about if the quantum
efficiency of the detector was halved. The noise performance of the
L3Vision devices is thus similar to the performance of a readout-noise
free device with half the quantum efficiency (see also
Mackay et al. (2001)).
If the photon flux per pixel read out is very low, electron multiplying CCDs operated at high gain can be used as photon-counting devices (rather like an array of avalanche photo-diodes). In this mode of operation, it should be possible to detect individual photons with high quantum efficiency. The performance of the devices for photon counting under these conditions will depend on the probability distribution for the output electrons.
Bob Tubbs 2003-11-14