Measurements of charge transfer efficiency at low signal levels

Measurements made with the camera at the NOT indicated that the charge transfer efficiency problems were limited to extremely low signal levels (less than one detected photon per pixel per frame). This strong non-linearity in the camera performance with the light level would make deconvolution of the affected images very difficult. A set of laboratory measurements was undertaken by Craig Mackay to investigate the charge transfer efficiency of the camera in detail at these low light levels in order to assist in the interpretation of our astronomical images.

Short exposure images were taken of a camera ``test card'' transparency using standard slide-copying optics, with a CCD65 detector in the camera. The voltage settings on the camera were such that the charge transfer efficiency deviated significantly from unity at low signal levels. At high signal levels the images of the test card showed a high degree of fine structure, ideal for charge transfer efficiency measurements.

Datasets of $1000$ images each were taken operating the CCD65 at high multiplication register gain with exposure times of $60$ $ms$ and $1$ $s$. In the test card images these light levels corresponded to $0.05$--$0.5$ photons per pixel per frame and $0.9$--$9.0$ photons per pixel per frame respectively. Ten exposures of $60$ $s$ were also taken with no multiplication register gain to provide an accurate representation of the test card at high signal level. There was no evidence for charge transfer efficiency problems in these long exposure images.

The raw images did not show any visual evidence for poor charge transfer efficiency, but the signal level was too low in the individual $60$ $ms$ exposures to make an accurate assessment. Software was written by the author to combine the short exposures and deconvolve the resulting images in order to make a quantitive assessment of the charge transfer efficiency.

The $60$ $ms$ exposures were co-added to increase the signal-to-noise, as were the $1$ $s$ and $60$ $s$ exposures. The summed images from the $60$ $ms$ and $1$ $s$ exposures were then deconvolved using the summed image from the long exposures in order to give a ``PSF'' which described the charge transfer efficiency problems at low light levels. The fraction of the signal residing a given number of pixels from the origin of this PSF corresponds to the fraction of electrons which have been displaced by this distance due to charge transfer efficiency problems. In order to control the noise in the deconvolution process, a 2-D version of the Nahman-Guillaume one parameter filter was used (Nahman & Guillaume, 1981). The filter parameter was adjusted until there was good dynamic range between the central peak of the PSF and the noise floor in the wings. In order to confirm that the filter was not adversely affecting the shape of the PSF, different long exposure images were deconvolved in the same way, providing a strongly peaked response at the origin which dropped to the noise floor within two pixels of the origin.

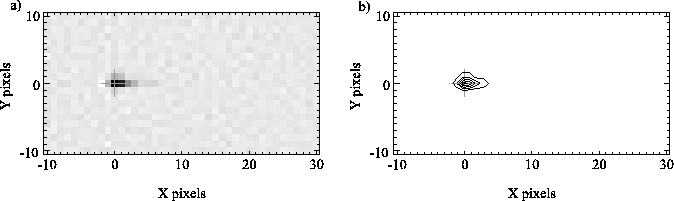
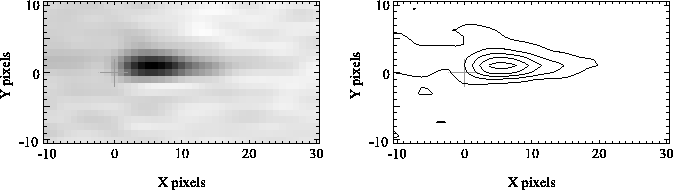
Figure 4.10 shows the result of deconvolving a section of the summed image from the $1$ $s$ exposures. The PSF shows a strong peak at the origin corresponding to those electrons which were transferred with good charge transfer efficiency. Weak tails extend both to the right and upwards, indicating that some of the photo-electrons are experiencing much poorer charge transfer efficiency for either horizontal or vertical transfers. With the shorter exposures (having fewer photons per pixel), the strong peak at the origin disappears, and the tails to the right and in the upwards direction are broadened and strongly enhanced to form a single peak offset from the origin, as shown by Figure 4.11.

Figure 4.10: A PSF describing the charge transfer efficiency for $1$ $s$ exposures at low light level - see main text for details. A section near centre of test card image was used for this measurement.

Figure 4.11: A PSF describing the charge transfer efficiency for $60$ $ms$ exposures at low light level. The same section of the test card was used as for Figure 4.10.

A PSF was calculated in this way for different regions of the test card image using the $60$ $ms$ exposures. The horizontal offset and vertical offset of the peak in the PSF was found to depend linearly on the horizontal position and vertical position respectively in the image. This is consistent with charge transfer efficiency problems in the image and store areas of the CCD, as electrons which are generated further from the readout register must undergo a larger number of transfers.

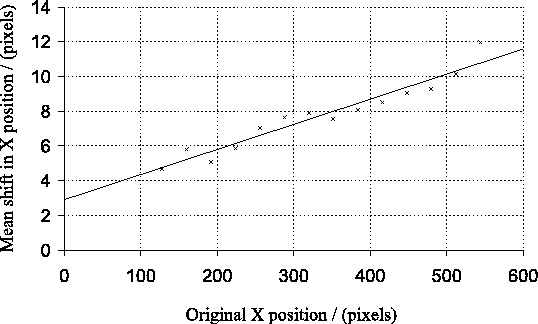
Figure 4.12 shows a plot of the horizontal offset in the PSF peak against the horizontal (``$x$'') position of the region used for the calculations. The data points are fit by a line which crosses the $x$-axis at an $x$ value of $-201$. This implies that a significant fraction of the charge transfer efficiency loss is occurring after the signal has left the image and store areas of the CCD, and is presumably occurring in the multiplication register. The bulk of the charge transfer efficiency losses do seem to occur in horizontal (serial) transfers in the store area of the CCD, however. The gradient of the line in Figure 4.12 indicates that electrons are being ``left behind'' in $1.4\%$ of the serial transfers in the store area of the CCD for these measurements.

Figure 4.12: Charge transfer efficiency for $60$ $ms$ exposures at low light level. The offset in the position of the image plotted on the vertical axis indicates the number of failed charge transfers. The position of the test card region used is proportional to the total number of serial transfers in the store area of the CCD required to transfer the photo-electrons to the multiplication register. The horizontal offset of the line would correspond to $201$ additional pixel transfers.

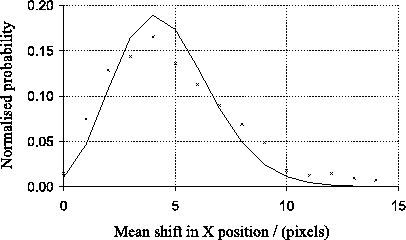
A cross section through the PSF calculated for a region centred on $x=128$ pixels is shown in Figure 4.13. The curve is similar in shape to the binomial distribution which would be expected if it was the result of $329$ transfers attempts, each having a $1.4\%$ chance of failing to transfer the electron.

Figure 4.13: Charge transfer efficiency for $60$ $ms$ exposures at low light level. A square region of the test card image was selected for this analysis. The region was centred $128$ pixels from the edge of the CCD in the horizontal (serial transfer) direction. The data shown in Figure 4.12 indicate that the offset in position for this region of the test card image was consistent with a $1.4\%$ CTE loss in $329$ transfers. The binomial distribution obtained for $329$ transfers with probability of $1.4\%$ for missing a transfer is shown.

The charge transfer efficiency was found to be strongly dependent on the (variable) operating voltages and environmental conditions of the camera. It was possible to get very good charge transfer efficiency in the laboratory with the CCD87 by selecting appropriate operating conditions. The operating voltages used during observations at the NOT are not precisely known, and for this reason it will not be possible to predict the charge transfer efficiency which was present for observations at the NOT.

The experimental measurements and calculations of charge transfer efficiency at low signal level are currently relatively time consuming, and require an image with suitably fine structure to be projected on to the CCD in a stable experimental setup. It would be extremely beneficial if an automated approach to this analysis could be developed which could be performed when the camera was at an astronomical telescope, so that the charge transfer efficiency could be maximised before astronomical observations began.