

Next: A Little Un-Learning
Up: An Outline of
Previous: An Outline of
A linear space is one upon which addition and scalar multiplication
are defined. Although such a space is often called a `vector
space', our use of the term `vector' will be reserved for the
geometric concept of a directed line segment. We still require
linearity, so that for any vectors  and
and 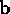 we must be able to
define their vector sum
we must be able to
define their vector sum 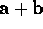 . Consistent with our purpose, we
will restrict scalars to be real numbers, and define the product of a
scalar
. Consistent with our purpose, we
will restrict scalars to be real numbers, and define the product of a
scalar 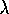 and a vector
and a vector  as
as 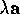 . We would like
this to have the geometrical interpretation of being a vector
`parallel' to
. We would like
this to have the geometrical interpretation of being a vector
`parallel' to  and of `magnitude'
and of `magnitude' 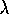 times the
`magnitude' of
times the
`magnitude' of  . To express algebraically the geometric idea
of magnitude, we require that an inner product be defined for
vectors.
. To express algebraically the geometric idea
of magnitude, we require that an inner product be defined for
vectors.
-
The inner product
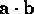 , also known as the dot or scalar
product, of two vectors
, also known as the dot or scalar
product, of two vectors  and
and 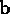 , is a scalar with
magnitude
, is a scalar with
magnitude 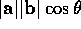 , where
, where 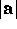 and
and
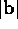 are the lengths of
are the lengths of  and
and 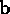 , and
, and 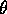 is the angle
between them. Here
is the angle
between them. Here 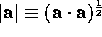 , so that the
expression for
, so that the
expression for 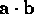 is effectively an algebraic definition of
is effectively an algebraic definition of
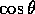 .
.
This product contains partial information about the relative direction
of any two vectors, since it vanishes if they are perpendicular. In
order to capture the remaining information about direction, another
product is conventionally introduced, the vector cross product.
-
The cross product
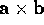 of two vectors is a
vector of magnitude
of two vectors is a
vector of magnitude 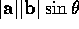 in the direction
perpendicular to
in the direction
perpendicular to  and
and 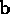 , such that
, such that  ,
, 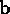 and
and 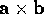 form a right-handed set.
form a right-handed set.
Mark Ashdown
 and
and 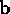 we must be able to
define their vector sum
we must be able to
define their vector sum 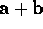 . Consistent with our purpose, we
will restrict scalars to be real numbers, and define the product of a
scalar
. Consistent with our purpose, we
will restrict scalars to be real numbers, and define the product of a
scalar 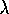 and a vector
and a vector  as
as 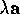 . We would like
this to have the geometrical interpretation of being a vector
`parallel' to
. We would like
this to have the geometrical interpretation of being a vector
`parallel' to  and of `magnitude'
and of `magnitude' 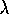 times the
`magnitude' of
times the
`magnitude' of  . To express algebraically the geometric idea
of magnitude, we require that an inner product be defined for
vectors.
. To express algebraically the geometric idea
of magnitude, we require that an inner product be defined for
vectors.
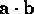 , also known as the dot or scalar
product, of two vectors
, also known as the dot or scalar
product, of two vectors  and
and 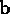 , is a scalar with
magnitude
, is a scalar with
magnitude 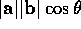 , where
, where 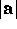 and
and
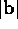 are the lengths of
are the lengths of  and
and 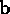 , and
, and 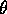 is the angle
between them. Here
is the angle
between them. Here 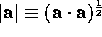 , so that the
expression for
, so that the
expression for 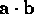 is effectively an algebraic definition of
is effectively an algebraic definition of
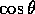 .
.
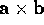 of two vectors is a
vector of magnitude
of two vectors is a
vector of magnitude 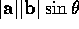 in the direction
perpendicular to
in the direction
perpendicular to  and
and 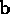 , such that
, such that  ,
, 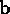 and
and 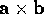 form a right-handed set.
form a right-handed set.