

Next: The Geometric Product
Up: An Outline of
Previous: How to Multiply
These products of vectors, together with their expressions in terms of
components (which we will not need or use here), form the basis of
everyday teaching in mathematical physics. In fact, the vector cross
product is an accident of our 3-dimensional world; in two dimensions
there simply isn't a direction perpendicular to  and
and 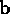 , and
in four or more dimensions that direction is ambiguous. A more general
concept is needed, so that full information about relative directions
can still be encoded in all dimensions. Thus, we will temporarily
un-learn the cross product, and instead introduce a new product, called
the outer product:
, and
in four or more dimensions that direction is ambiguous. A more general
concept is needed, so that full information about relative directions
can still be encoded in all dimensions. Thus, we will temporarily
un-learn the cross product, and instead introduce a new product, called
the outer product:
-
The outer product
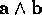 has magnitude
has magnitude 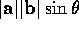 , but is not a scalar or a vector; it is a directed
area, or bivector, oriented in the plane containing
, but is not a scalar or a vector; it is a directed
area, or bivector, oriented in the plane containing  and
and
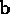 . The outer product has the same magnitude as the cross product
and shares its anticommutative (skew) property:
. The outer product has the same magnitude as the cross product
and shares its anticommutative (skew) property: 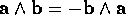 .
.
A way to visualise the outer product is to imagine 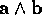 as the area `swept out' by displacing
as the area `swept out' by displacing  along
along 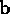 , with
the orientation given by traversing the parallelogram so formed first
along an
, with
the orientation given by traversing the parallelogram so formed first
along an  vector then along a
vector then along a 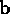 vector[4]. This
notion leads to a generalisation (due to Grassmann[21]) to
products of objects with higher dimensionality, or grade. Thus,
if the bivector
vector[4]. This
notion leads to a generalisation (due to Grassmann[21]) to
products of objects with higher dimensionality, or grade. Thus,
if the bivector 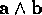 (grade 2) is swept out along another
vector
(grade 2) is swept out along another
vector  (grade 1), we obtain the directed volume element
(grade 1), we obtain the directed volume element 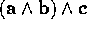 , which is a trivector (grade 3). By construction,
the outer product is associative:
, which is a trivector (grade 3). By construction,
the outer product is associative:
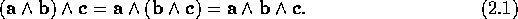
We can go no further in 3-dimensional space - there is nowhere else
to go. Correspondingly, the outer product of any four vectors 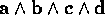 is zero.
is zero.
At this point we also drop the convention of
using bold-face type for vectors such as  - henceforth vectors
and all other grades will be written in ordinary type (with one specific
exception, discussed below).
- henceforth vectors
and all other grades will be written in ordinary type (with one specific
exception, discussed below).


Next: The Geometric Product
Up: An Outline of
Previous: How to Multiply
Mark Ashdown
 and
and 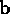 , and
in four or more dimensions that direction is ambiguous. A more general
concept is needed, so that full information about relative directions
can still be encoded in all dimensions. Thus, we will temporarily
un-learn the cross product, and instead introduce a new product, called
the outer product:
, and
in four or more dimensions that direction is ambiguous. A more general
concept is needed, so that full information about relative directions
can still be encoded in all dimensions. Thus, we will temporarily
un-learn the cross product, and instead introduce a new product, called
the outer product:
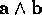 has magnitude
has magnitude 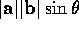 , but is not a scalar or a vector; it is a directed
area, or bivector, oriented in the plane containing
, but is not a scalar or a vector; it is a directed
area, or bivector, oriented in the plane containing  and
and
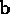 . The outer product has the same magnitude as the cross product
and shares its anticommutative (skew) property:
. The outer product has the same magnitude as the cross product
and shares its anticommutative (skew) property: 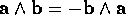 .
.
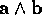 as the area `swept out' by displacing
as the area `swept out' by displacing  along
along 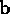 , with
the orientation given by traversing the parallelogram so formed first
along an
, with
the orientation given by traversing the parallelogram so formed first
along an  vector then along a
vector then along a 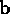 vector[4]. This
notion leads to a generalisation (due to Grassmann[21]) to
products of objects with higher dimensionality, or grade. Thus,
if the bivector
vector[4]. This
notion leads to a generalisation (due to Grassmann[21]) to
products of objects with higher dimensionality, or grade. Thus,
if the bivector 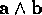 (grade 2) is swept out along another
vector
(grade 2) is swept out along another
vector  (grade 1), we obtain the directed volume element
(grade 1), we obtain the directed volume element 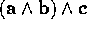 , which is a trivector (grade 3). By construction,
the outer product is associative:
, which is a trivector (grade 3). By construction,
the outer product is associative:
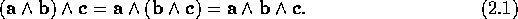
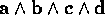 is zero.
is zero.
 - henceforth vectors
and all other grades will be written in ordinary type (with one specific
exception, discussed below).
- henceforth vectors
and all other grades will be written in ordinary type (with one specific
exception, discussed below).