 is a scalar and
is a scalar and 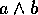 is a bivector
area, the inner and outer products respectively lower and raise the
grade of a vector. They also have opposite commutation properties:
is a bivector
area, the inner and outer products respectively lower and raise the
grade of a vector. They also have opposite commutation properties:
The inner and outer products of vectors are not the
whole story. Since  is a scalar and
is a scalar and 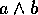 is a bivector
area, the inner and outer products respectively lower and raise the
grade of a vector. They also have opposite commutation properties:
is a bivector
area, the inner and outer products respectively lower and raise the
grade of a vector. They also have opposite commutation properties:

In this sense we can think of the inner and outer products together as forming the symmetric and antisymmetric parts of a new product, (defined originally by Grassmann[22] and Clifford[23]) which we call the geometric product, ab:

Thus, the product of parallel vectors is a scalar - we take such a product, for example, when finding the length of a vector. On the other hand, the product of orthogonal vectors is a bivector - we are finding the directed area of something. It is reasonable to suppose that the product of vectors that are neither parallel nor perpendicular should contain both scalar and bivector parts.
How on Earth do I Add a Scalar to a Bivector?
Most physicists need a little help at this point[2].
Adding together a scalar and a bivector doesn't seem right at first
- they are different types of quantities. But it is exactly what
you want an addition to do! The result of adding a scalar to a
bivector is an object that has both scalar and bivector parts, in
exactly the same way that the addition of real and imaginary numbers
yields an object with both real and imaginary parts. We call this
latter object a `complex number' and, in the same way, we shall
refer to a (scalar bivector) as a `multivector', accepting
throughout that we are combining objects of different types. The
addition of scalar and bivector does not result in a single new
quantity in the same way as 2 + 3 = 5; we are simply keeping track
of separate components in the symbol
bivector) as a `multivector', accepting
throughout that we are combining objects of different types. The
addition of scalar and bivector does not result in a single new
quantity in the same way as 2 + 3 = 5; we are simply keeping track
of separate components in the symbol 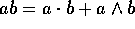 or z
= x + i y. This type of addition, of objects from separate linear
spaces, could be given the symbol
or z
= x + i y. This type of addition, of objects from separate linear
spaces, could be given the symbol 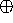 , but it should be evident
from our experience of complex numbers that it is harmless, and more
convenient, to extend the definition of addition and use the plain,
ordinary + sign.
, but it should be evident
from our experience of complex numbers that it is harmless, and more
convenient, to extend the definition of addition and use the plain,
ordinary + sign.
We have defined the geometric product in terms of the inner and outer
product of two vectors. An alternative and more mathematical approach
is to define the associative geometric product via a set of axioms and
introduce two `new' products 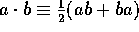 and
and 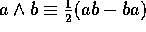 . Then, for example, if we
assert that the square of any vector should be a scalar, this would
allow us to prove that the product
. Then, for example, if we
assert that the square of any vector should be a scalar, this would
allow us to prove that the product  is scalar-valued, since
is scalar-valued, since
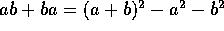 . This more axiomatic approach is taken in
Chapter 1 of Hestenes & Sobczyk[6].
. This more axiomatic approach is taken in
Chapter 1 of Hestenes & Sobczyk[6].