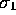 and
and 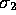 . These satisfy the
relations
. These satisfy the
relations
A 1-dimensional space has insufficient geometric structure to show
what is going on, so we begin in two dimensions, taking two
orthonormal basis vectors 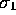 and
and 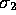 . These satisfy the
relations
. These satisfy the
relations
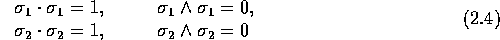
and

The outer product 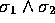 represents the directed area element of the
plane and we assume that
represents the directed area element of the
plane and we assume that  ,
,  are chosen such that this has
the conventional right-handed orientation. This completes the
geometrically meaningful quantities that we can make from these basis
vectors:
are chosen such that this has
the conventional right-handed orientation. This completes the
geometrically meaningful quantities that we can make from these basis
vectors:
We now assemble a Clifford algebra from these quantities. An arbitrary linear sum over the four basis elements in (2.6) is called a multivector. In turn, given two multivectors A and B, we can form their sum S = A + B by adding the components:
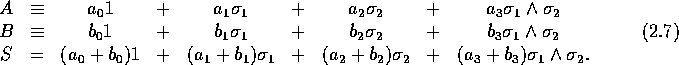
By this definition of a linear sum we have done almost nothing - the
power comes from the definition of the multiplication P = AB. In
order to define this product, we have to be able to multiply the 4
geometric basis elements. Multiplication by a scalar is obvious.
To form the products of the vectors we remember the
definition 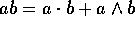 , so that
, so that
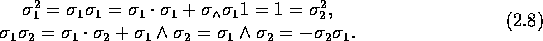
Products involving the bivector 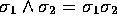 are particularly
important. Since the geometric product is associative, we
have:
are particularly
important. Since the geometric product is associative, we
have:
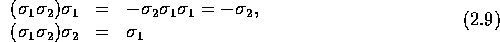
and

The only other product is the square of 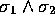 :
:
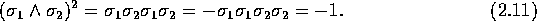
These results complete the definition of the product and enable, for example, the processes of addition and multiplication to be coded as computer functions. In principle, these definitions could be made an intrinsic part of a computer language, in the same way that complex number arithmetic is already intrinsic to some languages. To reinforce this point, it may be helpful to write out the product explicitly. We have,
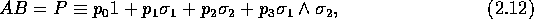
where
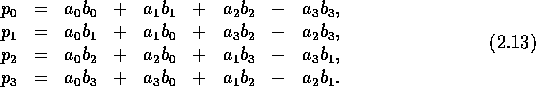
Multivector addition and multiplication obey the associative and distributive laws, so that we have, as promised, the geometric algebra of the plane.
We emphasise the important features that have emerged in the course of this derivation.
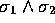 has the geometric effect of rotating the
vectors
has the geometric effect of rotating the
vectors 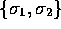 in its own plane by
in its own plane by 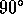 clockwise when
multiplying them on their left. It rotates vectors by
clockwise when
multiplying them on their left. It rotates vectors by 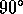 anticlockwise when multiplying on their right. This can be used to
define the orientation of
anticlockwise when multiplying on their right. This can be used to
define the orientation of 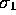 and
and 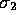 .
.
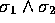 is a scalar:
is a scalar: 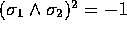 .
.
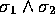 becomes our
first candidate for the role of the unit imaginary i, and in
2-dimensional applications it fulfills this role admirably. Indeed, we
see that the even-grade elements
becomes our
first candidate for the role of the unit imaginary i, and in
2-dimensional applications it fulfills this role admirably. Indeed, we
see that the even-grade elements 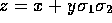 form a natural
subalgebra, equivalent to the complex numbers.
form a natural
subalgebra, equivalent to the complex numbers.