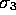If we now add a third orthonormal vector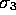 
to our basis set, we
generate the following geometrical objects:
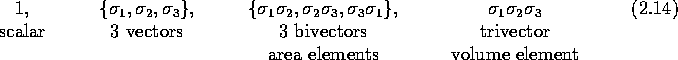
From these objects we form a linear space of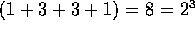 
dimensions, defining multivectors as before, together with the
operations of addition and multiplication. Most of the algebra is the
same as in the 2-dimensional version because the subsets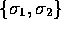 
, 
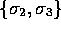and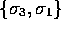 
generate 2-dimensional
subalgebras, so that the only new geometric products we have to
consider are
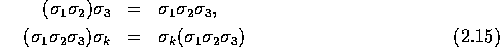
and
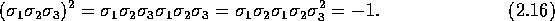
These relations lead to new geometrical insights:
,
but forms trivectors (volumes) with vectors perpendicular to it.
commutes with all vectors, and hence with
all multivectors.
also has the algebraic property of being a
square root of minus one. In fact, of the eight geometrical objects,
four have negative square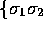 
, 
, 
, 
.
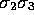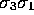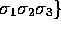Of these, the trivector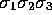 
is distinguished by its commutation
properties, and by the fact that it is the highest-grade element in
the space. Highest-grade objects are generically called
pseudoscalars, and 
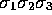is thus the unit pseudoscalar for
3-dimensional space. In view of its properties we give it the special
symbol i:
We should be quite clear, however, that we are using the symbol i to stand for a pseudoscalar, and thus cannot use the same symbol for the commutative scalar imaginary, as used for example in conventional quantum mechanics, or in electrical engineering. We shall use the symbol j for this uninterpreted imaginary, consistent with existing usage in engineering. The definition (2.17) will be consistent with our later extension to 4-dimensional spacetime.
