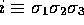 which has negative square and commutes with
all multivectors. Multiplying this by
which has negative square and commutes with
all multivectors. Multiplying this by 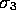 ,
, 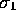 and
and 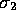 in turn we get
in turn we get
We have now reached the point which is liable to cause the greatest
intellectual shock. We have played an apparently harmless game with
the algebra of 3-dimensional vectors and found a geometric quantity 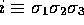 which has negative square and commutes with
all multivectors. Multiplying this by
which has negative square and commutes with
all multivectors. Multiplying this by 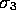 ,
, 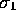 and
and 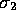 in turn we get
in turn we get
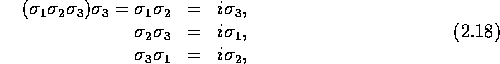
which is exactly the algebra of the Pauli spin matrices used in the
quantum mechanics of spin-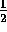 particles! The familiar Pauli
matrix relation,
particles! The familiar Pauli
matrix relation,

is now nothing more than an expression of the geometric product of orthonormal vectors. We shall demonstrate the equivalence with the Pauli matrix algebra explicitly in a companion paper[24], but here it suffices to note that the matrices
comprise a matrix representation of our 3-dimensional geometric algebra. Indeed, since we can represent our algebra by these matrices, it should now be obvious that we can indeed add together the various different geometric objects in the algebra - we just add the corresponding matrices. These matrices have four complex components (eight degrees of freedom), so we could always disentangle them again.
Now it is clearly true that any associative algebra can be
represented by a matrix algebra; but that matrix representation may
not be the best interpretation of what is going on. In the
quantum mechanics of spin-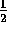 particles we have a
case where generations of physicists have been taught nothing but
matrices, when there is a perfectly good geometrical interpretation of
those same equations! And it gets worse. We were taught that the
particles we have a
case where generations of physicists have been taught nothing but
matrices, when there is a perfectly good geometrical interpretation of
those same equations! And it gets worse. We were taught that the 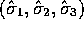 were the components of a vector
were the components of a vector 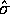 , and how to
write things like
, and how to
write things like 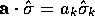 and
and
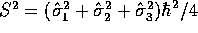 . But,
geometrically,
. But,
geometrically, 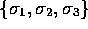 are three orthonormal vectors comprising
the basis of space, so that in
are three orthonormal vectors comprising
the basis of space, so that in 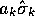 the
the 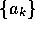 are the components of a vector along directions
are the components of a vector along directions 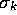 and
the result
and
the result 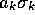 is a vector, not a scalar. With regard to
is a vector, not a scalar. With regard to
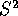 , if you want to find the length of a
vector, you must square and add the components of the vector along the
unit basis vectors - not the basis vectors themselves. So the result
, if you want to find the length of a
vector, you must square and add the components of the vector along the
unit basis vectors - not the basis vectors themselves. So the result
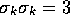 is certainly true, but does not have the
interpretation usually given to it.
is certainly true, but does not have the
interpretation usually given to it.
These considerations all indicate that our present thinking about quantum mechanics is infested with the deepest misconceptions. We believe, with David Hestenes, that geometric algebra is an essential ingredient in unravelling these misconceptions.
On the constructive side, the geometric algebra is easy to use, and
allows us to manipulate geometric quantities in a coordinate-free way.
The 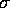 -vectors, which play an essential role, are
thereby removed from the mysteries of quantum mechanics, and used to
advantage in physics and engineering. We shall see that a similar
fate awaits Dirac's
-vectors, which play an essential role, are
thereby removed from the mysteries of quantum mechanics, and used to
advantage in physics and engineering. We shall see that a similar
fate awaits Dirac's 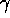 -matrices.
-matrices.
The algebra of 3-dimensional space, the Pauli algebra, is central to physics, and deserves further emphasis. It is an 8-dimensional linear space of multivectors, which we write as
where 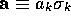 ,
, 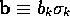 , and we have reverted
to bold-face type for 3-dimensional vectors. This is the exception
referred to earlier; we use this convention[5]
to maintain a visible difference between spacetime 4-vectors and
vectors of 3-dimensional space. There is never any ambiguity
concerning the basis vectors
, and we have reverted
to bold-face type for 3-dimensional vectors. This is the exception
referred to earlier; we use this convention[5]
to maintain a visible difference between spacetime 4-vectors and
vectors of 3-dimensional space. There is never any ambiguity
concerning the basis vectors 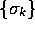 , however, and these will continue to
be written unbold.
, however, and these will continue to
be written unbold.
The space of even-grade elements of this algebra,

is closed under multiplication and forms a representation of the quarternion
algebra. Explicitly, identifying 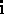 ,
, 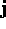 ,
, 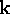 with
with
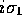 ,
, 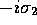 ,
, 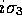 , respectively, we have the usual
quarternion relations, including the famous formula
, respectively, we have the usual
quarternion relations, including the famous formula

Finally in this section, we relearn the cross product in terms of the outer product and duality operation (multiplication by the pseudoscalar):

Here we have introduced an operator precedence convention in which an
outer or inner product always takes precedence over a geometric
product. Thus 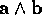 is taken before the multiplication by i.
is taken before the multiplication by i.
The duality operation in three dimensions interchanges a plane with a
vector orthogonal to it (in a right-handed sense). In the mathematical
literature this operation goes under the name of the `Hodge dual'.
Quantities like  or
or 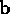 would conventionally be called `polar
vectors', while the `axial vectors' which result from cross-products can now
be seen to be disguised versions of bivectors.
would conventionally be called `polar
vectors', while the `axial vectors' which result from cross-products can now
be seen to be disguised versions of bivectors.