For this paper: postscript 2 Model... Abstract... 4 Effect on the ...

3 Cluster properties  

In this section, we model the formation of a very rich Abell cluster. The characteristics (see table 1) are chosen to be similar to those of the clusters described in Quilis et al. (1995) and Panek (1992) so that our results can be compared.

 
Table 1:  Cluster characteristics.

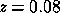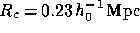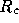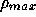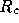The cluster is placed at a redshift , with a core radius ( is defined as the radius at which the cluster energy falls to one-half its maximum value). The maximal baryonic density encounter by an observed photon is taken to be and the baryon to dark-matter mass ratio is assumed to be 0.1. The -dependencies for and 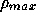ensure that the observed cluster characteristics (i.e. angular size and X-ray luminosity) are independent of the Hubble parameter. Throughout this paper we assume .

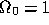Figure 3 shows the fluid density and the fluid velocity as a function of proper time as experienced by a photon which travels straight through the centre of the cluster. From the figure we see clearly that the fluid distributions are continuous.

 
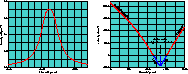
Figure 3:  Plot of the fluid density (left) and fluid velocity (right) as experienced by the photon while it is travelling through the Universe and the collapsing cluster. The horizontal axis marks the time prior to the present epoch in millions of years. We assume .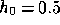

We next consider (fig 4) the density profile of the cluster at the time 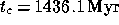ago, when the photon experienced the maximum density 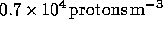. In order to check that the obtained density distribution is of realistic shape, we fit our profile to the equilibrium spherical King model (King (1966)):

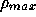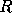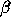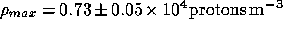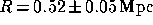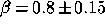where is the central density of the cluster, represents some core radius and is the conventional power-law index for such models. The results of a simple least-squares fit are , and . The result of this fit is very encouraging since it shows that our model leads to a radial density profile that matches quite closely those of observed clusters.

 
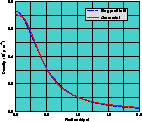
Figure 4:  Plot of the density when the photon is at the centre of the cluster. The obtained profile is realistic since it can be fitted by a spherical King model.