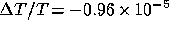 and
and 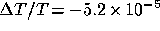 for
for
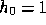 and
and 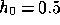 respectively. One notices that the distortion extends to
rather large projected angles (e.g.
respectively. One notices that the distortion extends to
rather large projected angles (e.g. 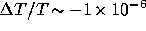 for an
observed angle of
for an
observed angle of  in the
in the 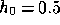 case). We may
also point out the fact that the anisotropy becomes slightly positive at large
angles.
case). We may
also point out the fact that the anisotropy becomes slightly positive at large
angles.
We now consider photon energy and concentrate on the CMB anisotropy produced when the photon passes through the cluster described in section 3. One must remember however that our model assumes a pressure-less fluid and so the cluster, in pure-infall, might evolves too rapidly. Therefore the temperature perturbations given in this section should be considered as upper limits.
Figure 5 shows the CMB anisotropy due to the gravitational
perturbation of the cluster described in table 1. The maximum
temperature distortion occurs at the centre of the cluster and has the value
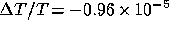 and
and 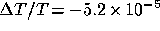 for
for
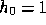 and
and 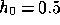 respectively. One notices that the distortion extends to
rather large projected angles (e.g.
respectively. One notices that the distortion extends to
rather large projected angles (e.g. 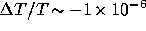 for an
observed angle of
for an
observed angle of 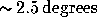 in the
in the 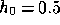 case). We may
also point out the fact that the anisotropy becomes slightly positive at large
angles.
case). We may
also point out the fact that the anisotropy becomes slightly positive at large
angles.
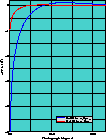
Figure 5: Temperature perturbation 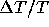 imprinted
on the CMB as a function of the observed angle from the centre of the cluster.
imprinted
on the CMB as a function of the observed angle from the centre of the cluster.
We can compare the central decrements calculated above with those of previous
authors. For Panek (1992) type I and type II clusters, the calculated central
decrements are 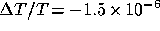 and
and 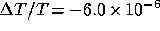 respectively, whereas Quilis et al. (1995) quote the decrement
respectively, whereas Quilis et al. (1995) quote the decrement 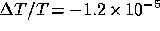 . For two cluster models with similar physical
properties Chodorowski (1991) finds
. For two cluster models with similar physical
properties Chodorowski (1991) finds 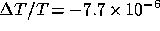 . Finally
Nottale (1984) used the SC model to predict a considerably larger central
decrement of
. Finally
Nottale (1984) used the SC model to predict a considerably larger central
decrement of 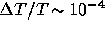 . However, this last value corresponds to
a very dense, unrealistic cluster. We can notice that, for
. However, this last value corresponds to
a very dense, unrealistic cluster. We can notice that, for 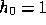 , our
predicted value is in rough agreement with Panek (1992) type II,
Chodorowski (1991) and Quilis et al. (1995). However our result for
, our
predicted value is in rough agreement with Panek (1992) type II,
Chodorowski (1991) and Quilis et al. (1995). However our result for 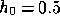 is about
five times larger since previous works predict the same value whatever is
is about
five times larger since previous works predict the same value whatever is
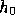 . We then suggest that, in such a Universe, the effect on CMB photons may
be more significant that previously stated.
. We then suggest that, in such a Universe, the effect on CMB photons may
be more significant that previously stated.