Proceedings of the Particle Physics and Early Universe
Conference (PPEUC).
For this paper:
 postscript
postscript
 4 Effect on the ...
4 Effect on the ...
 Abstract...
Abstract...
 6 Discussion...
6 Discussion...
5 Distant clusters
We consider, in this section, the formation of a massive cluster located at a
redshift 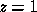 . It is more reasonable to apply our model for a distant cluster
rather than the one described in section 3. Indeed, at such
redshifts one could expect galaxy clusters to be in a formation process and
display large inward radial velocities. As from now, the cosmology is taken to
be
. It is more reasonable to apply our model for a distant cluster
rather than the one described in section 3. Indeed, at such
redshifts one could expect galaxy clusters to be in a formation process and
display large inward radial velocities. As from now, the cosmology is taken to
be 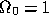 and
and 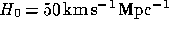 . The cluster
characteristics are the following:
. The cluster
characteristics are the following: 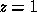 ,
, 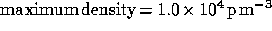 ,
, 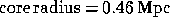 and the
mass within
and the
mass within 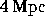 is
is 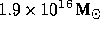 . In the
next section we investigate the lensing effect caused by such a cluster as well
as the effect imprinted on the CMB temperature and power spectrum.
. In the
next section we investigate the lensing effect caused by such a cluster as well
as the effect imprinted on the CMB temperature and power spectrum.
5.1 Gravitational lensing and effect on the CMB
A massive cluster such as described above is a powerful gravitational lens.
This effect is illustrated in figure 6. Our model also allows a
quantitative study of the effect of dynamically evolving lenses on the CMB
fluctuations. By simulating maps of fluctuations in the CMB due to inflation
and/or topological defects, we can investigate how features in these maps are
affected by the presence of the lens. As an example, figure 7 shows
the effect of our collapsing cluster on a CMB fluctuations realisation. The
result is a central decrease of temperature at the centre (i.e. 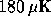 in our case) as well as a global magnification of the features.
in our case) as well as a global magnification of the features.
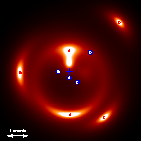
Figure 6: Lensing image of 4 sources at a redshift
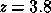 by the rich cluster described in section 5. The blue
bullets (A,B,C,D) show the positions of the sources as seen in the absence of
the cluster. The blue cross marks the centre of the cluster. The source A
placed on the lens caustic displays two images, one radially and the other
tangentially elongated.
by the rich cluster described in section 5. The blue
bullets (A,B,C,D) show the positions of the sources as seen in the absence of
the cluster. The blue cross marks the centre of the cluster. The source A
placed on the lens caustic displays two images, one radially and the other
tangentially elongated.
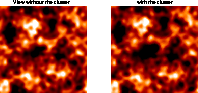
Figure 7: Effect of the collapsing cluster described in
section 5 on the CMB fluctuations. The first map is a simulation
of the CMB fluctuations due to inflation. The second one represents the same
patch of the sky (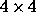 degrees) but with a rich cluster of galaxies at
its centre.
degrees) but with a rich cluster of galaxies at
its centre.
Aside from studying individual maps, we can also study the statistical effect
that a population of such lenses would have on the power spectrum of the CMB
fluctuations. This power spectrum is currently of immense theoretical and
observational interest, since it is now a possibility that the spectrum may be
measured, and so the values of cosmological constants may be found to
unprecedented accuracy. Such determinations depend, however, on distinctive
features in the power spectrum which may be affected by a population of large
clusters. Previous work on this effect has been performed such as
Seljak (1996), but we have now incorporated the effect of dynamically
collapsing clusters in a proper general relativistic fashion. Figure
8 gives the result obtained with the cluster used in the current
section.
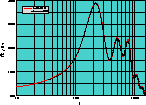
Figure 8: Effect on the CMB power spectrum of the rich
cluster described in section 5. We assume one cluster per 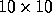 degrees field. The red curve is the unperturbed power spectrum as
the black dots represent the ``lensed'' spectrum.
degrees field. The red curve is the unperturbed power spectrum as
the black dots represent the ``lensed'' spectrum.
We find that the distinctive peaks in the power spectrum are slightly smoothed
out by such a population, and so this effect should be taken into account in
future analyses.
PPEUC Proceedings
Mon Jul 7 10:52:41 BST 1997
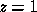 . It is more reasonable to apply our model for a distant cluster
rather than the one described in section 3. Indeed, at such
redshifts one could expect galaxy clusters to be in a formation process and
display large inward radial velocities. As from now, the cosmology is taken to
be
. It is more reasonable to apply our model for a distant cluster
rather than the one described in section 3. Indeed, at such
redshifts one could expect galaxy clusters to be in a formation process and
display large inward radial velocities. As from now, the cosmology is taken to
be 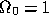 and
and 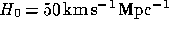 . The cluster
characteristics are the following:
. The cluster
characteristics are the following: 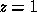 ,
, 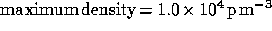 ,
, 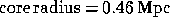 and the
mass within
and the
mass within 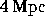 is
is 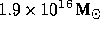 . In the
next section we investigate the lensing effect caused by such a cluster as well
as the effect imprinted on the CMB temperature and power spectrum.
. In the
next section we investigate the lensing effect caused by such a cluster as well
as the effect imprinted on the CMB temperature and power spectrum.
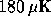 in our case) as well as a global magnification of the features.
in our case) as well as a global magnification of the features.

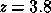 by the rich cluster described in section
by the rich cluster described in section 
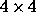 degrees) but with a rich cluster of galaxies at
its centre.
degrees) but with a rich cluster of galaxies at
its centre.
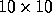 degrees field. The red curve is the unperturbed power spectrum as
the black dots represent the ``lensed'' spectrum.
degrees field. The red curve is the unperturbed power spectrum as
the black dots represent the ``lensed'' spectrum.