Normalising the short-timescale component of the autocorrelation
Early investigations of atmospheric timescales typically involved a
single high-speed photometer positioned at a single point in the image
plane of a telescope. The temporal autocorrelation of a time series of
measurements from such a device (i.e. the convolution of the time
series with itself) provides a useful time-domain representation of
the variance of the photometric flux with time. The long-timescale
component of the measured temporal autocorrelation is assumed by
Scaddan & Walker (1978) to be separable from the short-timescale
component. The long-timescale (low frequency) component varies
essentially linearly over the region of the autocorrelation which is
of interest to speckle imaging. The solid line in
Figure 2.1 shows a schematic representation of a
typical temporal autocorrelation curve. The long-timescale component
is indicated by the dashed line. In order to remove the effect of the
long-timescale component, a linear fit to this component is calculated
over the region of the temporal autocorrelation which is of interest
for speckle imaging. The measured autocorrelation is then divided by
this linear function to remove the long timescale component. The
result can then be rescaled so that it ranges from zero to unity, to
give the normalised high frequency component of the temporal
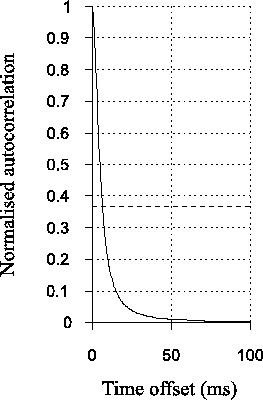
autocorrelation as shown in Figure 2.2. The
atmospheric timescale is the time delay over which this function
decays to 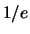 , defined by Roddier et al. (1982a); Vernin et al. (1991) as
, defined by Roddier et al. (1982a); Vernin et al. (1991) as 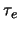 (but known as
(but known as
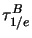 in Scaddan & Walker (1978)). In Figure
2.2,
in Scaddan & Walker (1978)). In Figure
2.2, 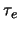 is marked by the crossing point
between the solid curve and dashed horizontal line.
is marked by the crossing point
between the solid curve and dashed horizontal line.
Figure 2.1:
Temporal autocorrelation for photometric measurements at a fixed point
(solid curve). The dashed line shows a linear fit to the
long-timescale fluctuations brought about by motion of the image
centroid.
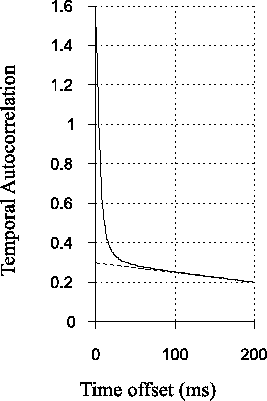 |
Figure 2.2:
Normalised temporal autocorrelation for photometric measurements at a
fixed point (solid curve). The dashed line marks a value of
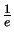 . The timescale
. The timescale 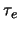 is
is 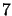
 in this example.
in this example.
 |
Bob Tubbs
2003-11-14

