Exposure selection from simulated data

In order to determine the performance of the Lucky Exposures technique under a variety of different conditions, the simulations described in Chapter 2.3.3 were used to generate a large number of short exposure images for each of the aperture diameters. The Strehl ratio of the short exposure images describes the fraction of the light which resides in a diffraction-limited core of the PSF. It is a very good indicator of how useful the exposures are for high-resolution imaging, as the light in the core of the PSF maps out the sky brightness distribution at high resolution, while the remaining light is distributed in the wings of the PSF and contributes largely to the noise in the image. In a speckled image the PSF core corresponds to the location of the brightest speckle. The offset in position of the PSF core and the distribution of light in the wings vary with the coherence timescale of the atmosphere. If a large number of short exposures are re-centred with respect to the core of the PSF and co-added, the contribution from the wings of the PSF will be averaged into a smooth halo, while the diffraction-limited information from the compact core of each PSF will remain (see e.g. Christou (1991)).

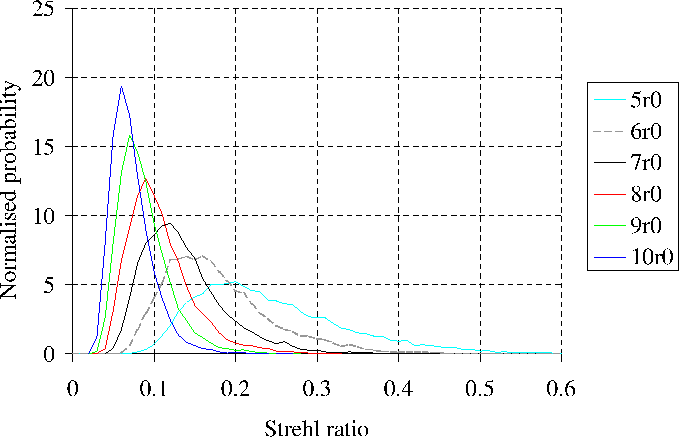
Figure 2.7 shows histograms of the measured Strehl ratios for the short exposures simulated with a variety of different aperture diameters (where the aperture diameter is described in terms of the atmospheric coherence length $r_{0}$). It is clear that the probability of obtaining a high Strehl ratio short exposure diminishes rapidly with increasing aperture size. If the investigator chooses to select the best $1\%$ of exposures of an unresolved source using an aperture of diameter $d=7r_{0}$, and to re-centred and co-add these exposures, the final image will have a Strehl ratio of $30$%--$35$%. There will be approximately twice as much light in a diffuse halo as is found in the core of the PSF. If the aperture diameter is increased slightly to $d=10r_{0}$, the PSF core in the selected exposures will be reduced slightly in diameter, but the diffuse halo will contain five times as much flux as the image core. For most imaging applications, the marginal gain in resolution is more than offset by the increased flux in the wings of the PSF, confirming that a $d\sim 7r_{0}$ aperture represents the largest which will provide high quality imaging using $1$% of the short exposures. If larger fractions of exposures are selected, it may be beneficial to use a slightly smaller aperture diameter.

Figure 2.7: Strehl ratios obtained from simulated short exposures with a range of different aperture diameters. The two atmospheric models gave similar distributions of Strehl ratios.

It is of interest to compare these results to the model of Fried (1978). He described the wavefronts entering a circular aperture in terms of the phase variance $\sigma_{\phi}^{2}$ from a best-fitted planar wavefront. Using Monte Carlo simulations, Fried calculated the probability that this variance $\sigma_{\phi}^{2}$ would be less than $1$ $radian^{2}$. From these results he produced the following model for the probability $P$ of good exposures:

$$P\simeq5.6\exp \left (-0.1557\left (\frac{d}{r_{0}}\right )^{2}\right )$$ (2.22)

given an aperture size $d$ greater than $3.5r_{0}$. Englander et al. (1983) compared the fraction of good images predicted by this model with the fraction of Lucky Exposures observed in ground-based imaging experiments and found agreement within the accuracy of the experimental measurements.

The instantaneous Strehl ratio on axis $\mathcal{S}_{a}$ obtained in the image plane of a simple imaging system can be determined by integrating the probability distribution for the wavefront phase variance across the aperture plane to give:

$$\mathcal{S}_{a}\sim\exp\left (-\sigma_{\phi}^{2}\right )$$ (2.23)

For small values of $\sigma_{\phi}^{2}$ this on-axis Strehl ratio will be approximately equal to the image Strehl ratio $\mathcal{S}$ which we are interested in.

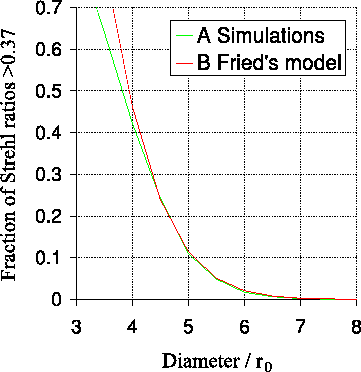
The criteria of selecting exposures when the phase variance $\sigma_{\phi}^{2}\le1$, Equation 2.23 would imply an image Strehl ratio $\mathcal{S}\mathrel{\hbox to 0pt{{\lower 3pt\hbox{$\mathchar''218$}}}\hss\raise 2.0pt\hbox{$\mathchar''13E$}}0.37$ (taking the approximation that the on-axis Strehl ratio represents the true Strehl ratio for the image). Figure 2.8 shows the fraction of exposures having a Strehl ratio greater than $0.37$ in my simulations plotted against Fried's model. There is excellent agreement for aperture diameters greater than $4r_{0}$.

Figure 2.8: Curve A shows the fraction of the exposures with a Strehl ratio greater than $0.37$ in each simulation, plotted against the aperture diameter measured in terms of the atmospheric coherence length $r_{0}$. Equation 2.22 is plotted as curve B. This is the model of Fried (1978) for the fraction of exposures where the wavefronts deviate by less than $1$ $radian$ RMS from a flat plane, and are expected to have Strehl ratios greater than than $0.37$.

One measure of image quality which incorporates both the Strehl ratio $S$ and the diffraction-limited resolution of the telescope diameter $d$ is the Strehl resolution $\mathcal{R}$, defined as:

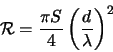$$\mathcal{R}=\frac{\pi S}{4}\left (\frac{d}{\lambda}\right )^2$$ (2.24)

If the best 1% of exposures are selected, Hecquet & Coupinot (1985) showed that the Strehl resolution achieved is greatest for apertures with diameters between $4r_{0}$ and $7r_{0}$. The Strehl resolution decreases relatively quickly for apertures larger than $7r_{0}$. The Strehl resolution does not represent a true measure of the image resolution in this application as the FWHM of the PSF core continues to get smaller with increasing aperture diameter beyond $d=7r_{0}$. The Strehl ratio and image FWHM separately provide a more useful description of the short exposure images, and I will generally use these parameters in describing the quality of the PSF.