The Kolmogorov model of turbulence
A description of the nature of the wavefront perturbations introduced
by the atmosphere is provided by the Kolmogorov model developed
by Tatarski (1961), based partly on the studies of turbulence by the
Russian mathematician Andreï Kolmogorov
(Kolmogorov, 1941a,b). This model is supported by a variety of
experimental measurements
(e.g. Colavita et al. (1987); Nightingale & Buscher (1991); Buscher et al. (1995); O'Byrne (1988)) and is widely used in
simulations of astronomical imaging. The model assumes that the
wavefront perturbations are brought about by variations in the
refractive index of the atmosphere. These refractive index variations
lead directly to phase fluctuations described by
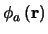 , but any amplitude fluctuations are only
brought about as a second-order effect while the perturbed wavefronts
propagate from the perturbing atmospheric layer to the telescope. For
all reasonable models of the Earth's atmosphere at optical and
infra-red wavelengths the instantaneous imaging performance is
dominated by the phase fluctuations
, but any amplitude fluctuations are only
brought about as a second-order effect while the perturbed wavefronts
propagate from the perturbing atmospheric layer to the telescope. For
all reasonable models of the Earth's atmosphere at optical and
infra-red wavelengths the instantaneous imaging performance is
dominated by the phase fluctuations
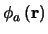 . The amplitude fluctuations described by
. The amplitude fluctuations described by
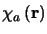 have negligible effect on the
structure of the images seen in the focus of a large telescope.
have negligible effect on the
structure of the images seen in the focus of a large telescope.
The phase fluctuations in Tatarski's model are usually assumed to have
a Gaussian random distribution with the following second order
structure function:
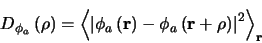 |
(1.3) |
where
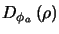 is the
atmospherically induced variance between the phase at two parts of the
wavefront separated by a distance
is the
atmospherically induced variance between the phase at two parts of the
wavefront separated by a distance 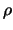 in the aperture
plane, and
in the aperture
plane, and
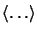 represents the ensemble average.
represents the ensemble average.
The structure function of Tatarski (1961) can be described in terms
of a single parameter  :
:
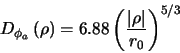 |
(1.4) |
 indicates the ``strength'' of the phase fluctuations as it
corresponds to the diameter of a circular telescope aperture at which
atmospheric phase perturbations begin to seriously limit the image
resolution. Typical
indicates the ``strength'' of the phase fluctuations as it
corresponds to the diameter of a circular telescope aperture at which
atmospheric phase perturbations begin to seriously limit the image
resolution. Typical  values for I band (
values for I band (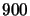
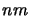 wavelength)
observations at good sites are
wavelength)
observations at good sites are 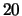 --
--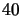
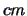 . Fried (1965) and
Noll (1976) noted that
. Fried (1965) and
Noll (1976) noted that  also corresponds to the aperture
diameter for which the variance
also corresponds to the aperture
diameter for which the variance 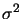 of the wavefront phase
averaged over the aperture comes approximately to unity:
of the wavefront phase
averaged over the aperture comes approximately to unity:
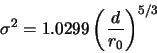 |
(1.5) |
Equation 1.5 represents a commonly used definition for
 .
.
A number of authors
(e.g. Mandelbrot (1974); Kuo & Corrsin (1972); Siggia (1978); Frisch et al. (1978); Kim & Jaggard (1988)) have
suggested alternatives to this Gaussian random model designed to
better describe the intermittency of turbulence discovered by
Batchelor & Townsend (1949). Although variations in seeing conditions have been
found on timescales of minutes and hours
(Wilson, 2003; Racine, 1996; Vernin & Muñoz-Tuñón, 1998), no significant experimental evidence has
been put forward which strongly favours any one of the intermittency
models for the turbulence involved in astronomical seeing. The
Gaussian random model is still the most widely used, and will be the
principal model discussed in this thesis.
Subsections
Bob Tubbs
2003-11-14
![]() :
:
![]() .
.