In reality, phase fluctuations in the atmosphere are only expected to
follow the structure function shown in
Equation 1.4 over a finite range of length
scales. The turbulent energy is injected at large scales by wind
shear. The bulk of the wind shear is expected in discrete layers of
the atmosphere, and the largest turbulent structures are expected to
fit within one of these atmospheric layers. The length scale at which
the structure function for Kolmogorov turbulence breaks down at large
scales is called the outer scale of turbulence. Several attempts have
been made at measuring the size of this outer scale using a variety of
different methods (see e.g.
Nightingale & Buscher (1991); Linfield et al. (2001); Coulman et al. (1988); Martin et al. (2000); Ziad et al. (1994); Davis et al. (1995); Wilson et al. (1999); Buscher et al. (1995)),
but there has been substantial variation in the measured values. The Von
Karman model (Ishimaru, 1978) is expected to describe the form of
the power spectrum for phase fluctuations on length scales larger than
the outer scale. If
the outer scale is larger than the telescope diameter, then most of
the properties of short exposure astronomical images will not depend
significantly on the precise size of the outer scale (although the
amplitude of image motion is still weakly dependent on the outer scale
size). The remaining uncertainty in the size of the outer scale has
little impact on the work presented in this thesis.
At small scales (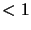
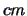) the turbulent energy in the atmosphere is
dissipated through the viscosity of the air (Roddier, 1981). The
length scale at which this becomes significant is called the inner scale of turbulence. The steepness of the Kolmogorov turbulence
spectrum means that any reduction in the power at such small length
scales has relatively little effect on the imaging performance of
optical and infra-red telescopes, and I will not discuss the inner
scale any further in this thesis.
Bob Tubbs
2003-11-14
