Simulations of the CCD65 L3Vision device with 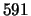 gain stages were
first undertaken using model 1 for the individual gain stages (where
the additional impact ionisation electrons were chosen from a Poisson
distribution). In the simulations the same value of the gain
gain stages were
first undertaken using model 1 for the individual gain stages (where
the additional impact ionisation electrons were chosen from a Poisson
distribution). In the simulations the same value of the gain 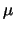 was
used for each of the
was
used for each of the 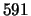 stages. The total gain of the
multiplication register was thus given by
stages. The total gain of the
multiplication register was thus given by 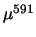 . The three
simulations used three different values of
. The three
simulations used three different values of 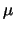 chosen to give total
multiplication register gains
chosen to give total
multiplication register gains 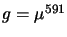 of
of 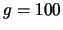 ,
, 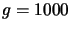 and
and
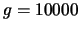 . The probability distributions for the output electrons in
these three simulations are shown in
Figure 4.2.
. The probability distributions for the output electrons in
these three simulations are shown in
Figure 4.2.
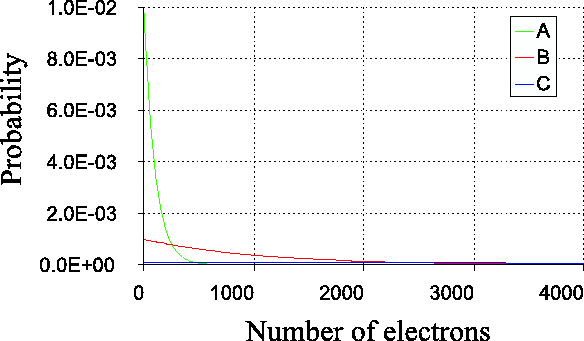
Figure 4.2:
The probability distribution for the number of output electrons from a
multiplication register of 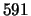 stages with a single electron input
and total register gains of
stages with a single electron input
and total register gains of 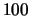 ,
, 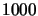 and
and 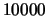 (curves A, B and
C respectively). All three probability curves fall to zero for the
case of less than one output electron. For these simulations model 1
was used for the individual gain stages, where additional electrons
are selected from a Poisson distribution. The same data are plotted on
a logarithmic scale in Figure 4.3.
(curves A, B and
C respectively). All three probability curves fall to zero for the
case of less than one output electron. For these simulations model 1
was used for the individual gain stages, where additional electrons
are selected from a Poisson distribution. The same data are plotted on
a logarithmic scale in Figure 4.3.
 |
The probability distributions for the output electrons are well
approximated by decaying exponential curves for large values of
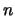 . This is highlighted in Figure 4.3a
where the curves are plotted on a logarithmic scale. The probability
curves appear as straight lines over a wide range of
. This is highlighted in Figure 4.3a
where the curves are plotted on a logarithmic scale. The probability
curves appear as straight lines over a wide range of 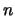 in the
plot. For very large values of
in the
plot. For very large values of 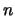 the probability reaches the
computational accuracy of the software corresponding to a value of
the probability reaches the
computational accuracy of the software corresponding to a value of
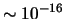 , and beyond this point the probability calculations are
dominated by noise. Figure 4.3b shows an
expanded view of the probability distributions for small
, and beyond this point the probability calculations are
dominated by noise. Figure 4.3b shows an
expanded view of the probability distributions for small
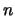 . Exponential curves were least-squares fitted to the probability
curves for the large
. Exponential curves were least-squares fitted to the probability
curves for the large 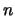 region, and these are extrapolated as dashed
curves in this plot. For small values of
region, and these are extrapolated as dashed
curves in this plot. For small values of 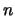 (
(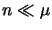 ) the
probability curve begins to fall very slightly below the best fit
exponential before dropping rapidly to zero for
) the
probability curve begins to fall very slightly below the best fit
exponential before dropping rapidly to zero for 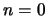 .
.
Figure 4.3:
The probability distributions from Figure 4.2
plotted on a logarithmic scale. A multiplication register of 591
stages was simulated with a single electron input and total register
gains of 100, 1000 and 10000 (curves A, B and C respectively). Model 1
was used for the individual gain stages, where additional electrons
are selected from a Poisson distribution. Panel b) shows an
enlargement of one portion of the plot in panel
a). The curves in panel a) were well fitted with
exponential functions for the case of large numbers of output
electrons, and these fits have been extrapolated as dashed lines in
panel b).
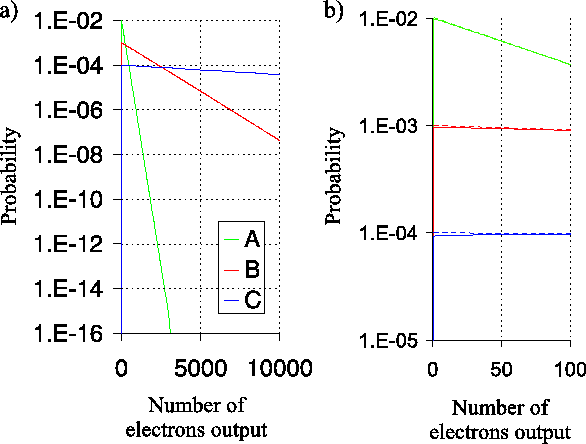 |
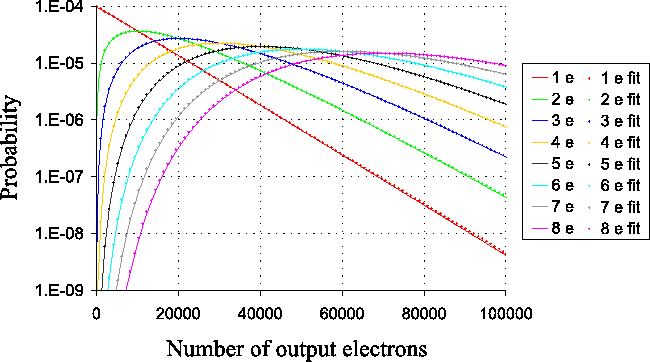
Figure 4.4 shows similar plots for a
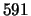 stage register with overall gain
stage register with overall gain 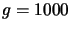 with different numbers
of input electrons. The general shape of the curves was not strongly
dependent on the number of gain stages
with different numbers
of input electrons. The general shape of the curves was not strongly
dependent on the number of gain stages 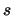 as long as
as long as 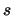 was large.
was large.
Figure 4.4:
The probability distribution for the number of output electrons from a
multiplication register of 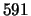 stages with different numbers of
input electrons. The discrete points on the graph show selected values
from the numerical fit described by
Equation 4.27, as discussed in the text.
stages with different numbers of
input electrons. The discrete points on the graph show selected values
from the numerical fit described by
Equation 4.27, as discussed in the text.
 |
Based upon the exponential fits in
Figure 4.3, we can say that the
probability distributions for the number of output electrons produced
when one input electron enters an electron multiplying CCD with a
large number of gain stages can be approximated by the function:
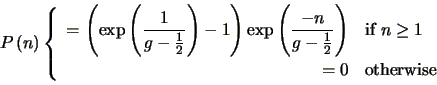 |
(4.25) |
where 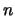 is an integer describing the number of output electrons and
is an integer describing the number of output electrons and
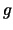 is the overall gain of the multiplication register.
is the overall gain of the multiplication register.
If we approximate Equation 4.25 as a
continuous function and convolve it with itself we get an
approximation for the probability distribution given two input
electrons:
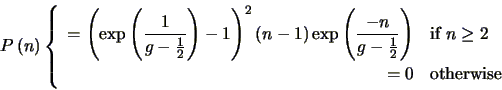 |
(4.26) |
With further convolutions, and taking approximations for the case of
large gain 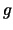 and a large number
and a large number 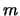 of input electrons, I obtained
the following model for the probability distribution for the output
electrons:
of input electrons, I obtained
the following model for the probability distribution for the output
electrons:
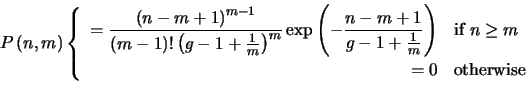 |
(4.27) |
where 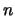 is the number of output electrons. Individual data points
calculated using this equation are included in
Figure 4.4 alongside the appropriate
probability curves calculated numerically for model 1. The
approximation described by Equation 4.27
does not differ substantially from the numerically calculated curves
even for one or two input electrons (although slightly better
approximations for one and two input electrons are given by
Equations 4.25 and
4.26 respectively).
is the number of output electrons. Individual data points
calculated using this equation are included in
Figure 4.4 alongside the appropriate
probability curves calculated numerically for model 1. The
approximation described by Equation 4.27
does not differ substantially from the numerically calculated curves
even for one or two input electrons (although slightly better
approximations for one and two input electrons are given by
Equations 4.25 and
4.26 respectively).
Bob Tubbs
2003-11-14

![]() . This is highlighted in Figure 4.3a
where the curves are plotted on a logarithmic scale. The probability
curves appear as straight lines over a wide range of
. This is highlighted in Figure 4.3a
where the curves are plotted on a logarithmic scale. The probability
curves appear as straight lines over a wide range of ![]() in the
plot. For very large values of
in the
plot. For very large values of ![]() the probability reaches the
computational accuracy of the software corresponding to a value of
the probability reaches the
computational accuracy of the software corresponding to a value of
![]() , and beyond this point the probability calculations are
dominated by noise. Figure 4.3b shows an
expanded view of the probability distributions for small
, and beyond this point the probability calculations are
dominated by noise. Figure 4.3b shows an
expanded view of the probability distributions for small
![]() . Exponential curves were least-squares fitted to the probability
curves for the large
. Exponential curves were least-squares fitted to the probability
curves for the large ![]() region, and these are extrapolated as dashed
curves in this plot. For small values of
region, and these are extrapolated as dashed
curves in this plot. For small values of ![]() (
(![]() ) the
probability curve begins to fall very slightly below the best fit
exponential before dropping rapidly to zero for
) the
probability curve begins to fall very slightly below the best fit
exponential before dropping rapidly to zero for ![]() .
.

![]() stage register with overall gain
stage register with overall gain ![]() with different numbers
of input electrons. The general shape of the curves was not strongly
dependent on the number of gain stages
with different numbers
of input electrons. The general shape of the curves was not strongly
dependent on the number of gain stages ![]() as long as
as long as ![]() was large.
was large.

![]() and a large number
and a large number ![]() of input electrons, I obtained
the following model for the probability distribution for the output
electrons:
of input electrons, I obtained
the following model for the probability distribution for the output
electrons: