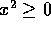The spacetime of Einstein's relativity is 4-dimensional, but with a
difference. So far we have assumed that the square of any vector x
is a scalar, and that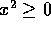 
. For spacetime it is appropriate to make a different choice. We take
the (+ - - -) metric usually preferred by physicists, with
a basis for the spacetime algebra[20] (STA) made up by the
orthonormal vectors
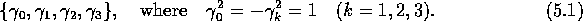
These vectors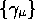 
obey the same algebraic relations as Dirac's
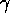-matrices, but our interpretation of them is not that of
conventional relativistic quantum mechanics. We do not view these
objects as the components of a strange vector of matrices, but (as
with the Pauli matrices of 3-space) as four separate vectors, with a
clear geometric meaning.
From this basis set of vectors we construct the 16 (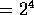
)
geometric elements of the STA:
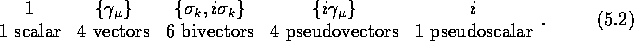
The time-like bivectors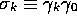 
are isomorphic to
the basis vectors of 3-dimensional space; in the STA they represent an
orthonormal frame of vectors in space relative to the laboratory
time vector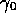 
[5,20]. The unit pseudoscalar of
spacetime is defined as
which is indeed consistent with our earlier definition.
The geometric properties of spacetime are built into the mathematical
language of the STA - it is the natural language of relativity.
Equations written in the STA are invariant under passive
coordinate transformations. For example, we can write the vector x
in terms of its component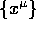s 
as
These components depend on the frame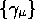 
and change under
passive transformations, but the vector x is itself invariant.
Conventional methods already make good use of scalar invariants in
relativity, but much more power is available using the STA.
Active transformations are performed by rotors R, which are again
even multivectors satisfying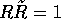 
:
where the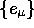 
comprise a new frame of orthogonal vectors.
Any rotor R can be written as
where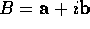 
is an arbitrary 6-component bivector (
and
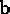are relative vectors). When performing rotations in higher
dimensions, a simple rotation is defined by a plane, and cannot
be characterised by a rotation axis; it is an accident of
3-dimensional space that planes can be mapped to lines by the duality
operation. Geometric algebra brings this out clearly by expressing a
rotation directly in terms of the plane in which it takes place.
For the 4-dimensional generalisation of the gradient operator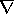 
, we
take account of the metric and write
where the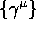 
are a reciprocal frame of
vectors to the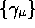 
, defined via
.
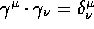As an example of the use of STA, we consider electromagnetism, writing the electromagnetic field in terms of the 4-potential A as
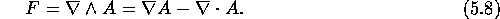
The divergence term 
is zero in the Lorentz gauge. The
field bivector F is expressed in terms of the more familiar
electric and magnetic fields by making a space-time split in the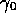 
frame:
where
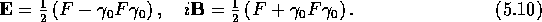
Particularly striking is the fact that Maxwell's equations[20,27] can be written in the simple form
where J is the 4-current. Equation 5.11 contains all of
Maxwell's equations because the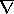 
operator is a vector and F
is a bivector, so that the geometric product has both vector and
trivector components. This trivector part is identically zero in the
absence of magnetic charges. It is worth emphasising[5]
that this compact formula (5.11) is not just a trick of notation,
because the 
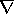operator is invertible. We can, therefore, solve
for F:
The inverse operator is known to physicists in the guise of the Green's propagators of relativistic quantum mechanics. We return to this point in a companion paper[16], in which we demonstrate this inversion explicitly for diffraction theory.
It is possible here, as in three dimensions, to represent a
relativistic quantum-mechanical spinor (a Dirac spinor) by the
even subalgebra of the STA[7,24], which is
8-dimensional. We write this spinor as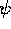 
and, since 
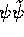contains only grade-0 and grade-4 terms, we decompose 
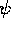as
where R is a spacetime rotor. Thus, a relativistic spinor also contains an instruction to rotate - in this case to carry out a full Lorentz rotation. The monogenic equation in spacetime is simply
which, remarkably, is also the STA form of the massless Dirac equation[24]. Furthermore, the inclusion of a mass term requires only a simple modification:
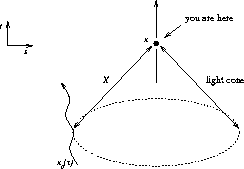
Figure 2: A charge moving in the observer's past light-cone
As a final example of the power of the STA in relativistic physics, we give a
compact formula for the fields of a radiating charge. This derivation is as
explicit as possible, in order to give readers new to the STA some feeling for
its character, but nevertheless it is still as compact as any of the
conventional treatments in the literature. Let a charge q move along a
world-line defined by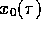 
, where 
is proper time. An observer
at spacetime position x receives an electromagnetic influence from the
charge when it lies on that observer's past light-cone
(see Figure 2). The vector
is the separation vector down the light-cone, joining the observer to
this intersection point. We can take equation (5.16),
augmented by the condition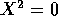 
, to define a mapping from the
spacetime position x to a value of the particle's proper time
. In this sense, we can write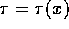 
, and treat 
as a scalar field. If the charge is at rest in the observer's frame
we have
where r is the 3-space distance from the observer to the charge
(taking c=1). For this simple case the 4-potential A is a
pure 
electrostatic field, which we can write as
because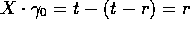 
. Generalising to an arbitrary
velocity v for the charge, relative to the observer, gives
which is a particularly compact and clear form for the Liénard-Wiechert potential.
We now wish to differentiate the potential to find the Faraday
bivector. This will involve some general results concerning
differentiation in the STA, which we now set up; for further useful
results see Chapter 2 of Hestenes & Sobczyk[6]. Since the
gradient operator is a vector we must take account of its commutation
properties. Though it is evident that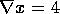 
, we need also to
deal with expressions such as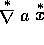 
, where a is a
vector, and where the stars indicate that the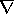 
operates only
on x rather than a. The result[6] is found by
anticommuting the x past the a to give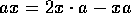 
, and then
differentiating this. Generalized to a grade-r
multivector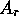 
in an n-dimensional space, we have
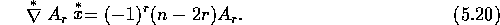
Thus, in the example given above,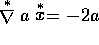 
. (See equation
(4.20) for a 3-dimensional application of this result.)
We will also need to exploit the fact that the chain rule applies in the STA as in ordinary calculus, so that (for example)
since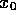 
is a function of 
alone, and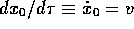 
is the particle velocity. In equation (5.21)
we use the convention that (in the absence of brackets or overstars)
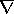only operates on the object immediately to its right.
Armed with these results, we can now proceed quickly to the Faraday bivector. First, since
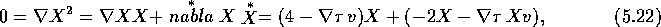
it follows that
As an aside, finding an explicit expression for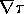 
confirms
that the particle proper time can be treated as a scalar field -
which is, perhaps, a surprising result. In the terminology of Wheeler
& Feynman[28], such a function is called an `adjunct field',
because it obviously carries no energy or charge, being merely a
mathematical device for encoding information. We share the hope of
Wheeler & Feynman that some of the paradoxes of classical and quantum
electrodynamics, in particular the infinite self-energy of a point charge,
might be avoidable by working with adjunct fields of this kind.
To differentiate A, we need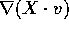 
. Using the results already
established we have
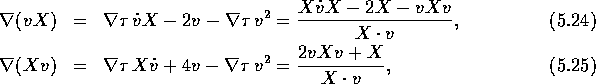
which combine to give
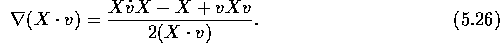
This yields
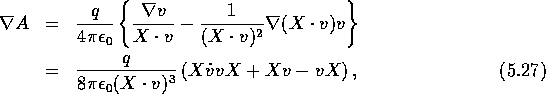
so that
and
Here,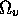 
is the `acceleration bivector' of the particle:
The quantity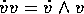 
is a pure bivector, because
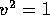implies that 
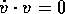. For more on the value
of representing the acceleration in terms of a bivector, and
the sense in which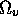 
is the rest-frame component of a
more general acceleration bivector, see Chapter 6 of Hestenes &
Sobczyk[6].
The form of the Faraday bivector given by equation faraday is very
revealing. It displays a clean split into a velocity term proportional
to 
and a long-range radiation term
proportional to 
. The first term is exactly the
Coulomb field in the rest frame of the charge, and the radiation term,
is proportional to the rest-frame acceleration projected down the null-vector X.
Finally, we return to the subject of adjunct fields. Clearly X is an
adjunct field, as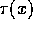 
was. It is easy to show that
so that
In this expression for F we have expressed a physical field solely in terms of a derivative of an `information carrying' adjunct field. Expressions such as (5.32) and (5.33) (which we believe are new, and were derived independently by ourselves and David Hestenes) may be of further interest in the elaboration of Wheeler-Feynman type `action at a distance' ideas[28,29].
