Limiting magnitude of reference source for speckle interferometry

A number of high resolution imaging techniques exist which involve Fourier analysis of individual short exposure images taken at a large telescope (see e.g. Roddier (1988)). Only those methods which preserve some Fourier phase information from the source can be used to produce true astronomical images, and the techniques which preserve Fourier phase information require higher light levels than the Lucky Exposures and shift-and-add methods (see e.g. Roddier (1988); Chelli (1987)). These methods are thus limited to a smaller range of astronomical targets. 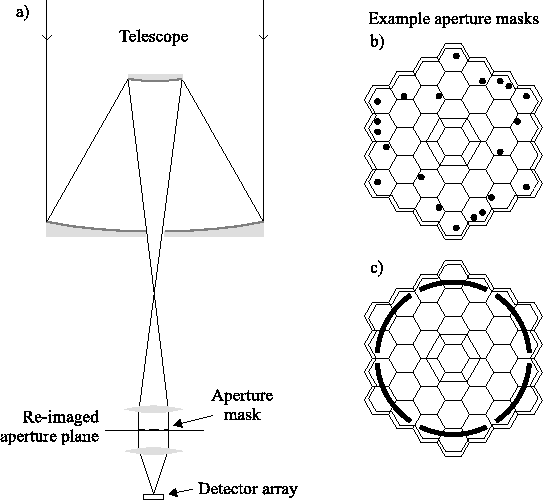The bispectral analysis (speckle masking) method has often been applied to data taken through masked apertures, where most of the aperture is blocked off and light can only pass through a series of small holes (subapertures). For simplicity these aperture masks are usually either placed in front of the secondary (e.g. Tuthill et al. (2000)) or placed in a re-imaged aperture plane as shown in Figure 1.6a (e.g. Haniff et al. (1987); Young et al. (2000); Baldwin et al. (1986)). The masks are usually categorised either as non-redundant or partially redundant. Non-redundant masks consist of arrays of small holes where no two pairs of holes have the same separation vector. Each pair of holes provides a set of fringes at a unique spatial frequency in the image plane. Partially redundant masks are usually designed to provide a compromise between minimising the redundancy of spacings and maximising both the throughput and the range of spatial frequencies investigated (Haniff & Buscher, 1992; Haniff et al. , 1989). Figures 1.6b and 1.6c show examples of aperture masks used in front of the secondary at the Keck telescope by Peter Tuthill and collaborators; Figure 1.6b is a non-redundant mask while Figure 1.6c is partially redundant. Although the signal-to-noise at high light level can be improved with aperture masks, the limiting magnitude cannot be significantly improved for photon-noise limited detectors (see Buscher & Haniff (1993)).

Figure 1.6: a) shows a simple experiment using an aperture mask in a re-imaged aperture plane. b) and c) show diagrams of aperture masks which were placed in front of the secondary mirror of the Keck telescope by Peter Tuthill and collaborators. The solid black shapes represent the subapertures (holes in the mask). A projection of the layout of the Keck primary mirror segments is overlaid.