The effect of mirror aberrations

Adjustments to the primary mirror supports of the NOT by Michael Anderson and Anton Sørensen (Andersen & Sørensen, 1996; Sørensen, 2002) are understood to have given the NOT an extremely good mirror figure for zenith angles less than $\sim50^{\circ}$. After the adjustments had been made the small residual errors were found to vary with telescope pointing, but a detailed description of these variations is not available to me at the time of writing.

In order to investigate the possible impact of any remaining aberrations, I undertook simulations with various different levels of mirror aberration. In the absence of direct measurements of the mirror shape after the adjustment to the actuators had been made I have suggested two models for the mirror aberrations as follows:

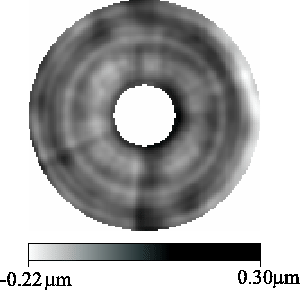
Model 1 represents a ``worst-case scenario'', with no improvement to the mirror aberrations after adjustment of the mirror supports. The mirror aberrations are taken directly from measurements of wavefront curvature made before the mirror actuators were adjusted (these measurements were provided by Sørensen (2002)). There is no defocus component in the model. The wavefront errors are shown as a function of position in the aperture plane in Figure 3.2.

Model 2 is identical to model 1 except that mirror aberrations on scales larger than the mean separation between adjacent mirror supports have been strongly suppressed. It is intended to represent a ``best-case scenario'', with near-optimal corrections to the mirror supports. The wavefront errors for model 2 are shown in Figure 3.3. It is understood that the residual wavefront errors at the NOT were small after the mirror actuators had been adjusted, hence the real shape of the primary mirror was probably similar to that shown in model 2.

Figure 3.2: Greyscale map of the phase aberrations in the NOT aperture provided by Sørensen (2002).

Figure 3.3: Phase map of the NOT aberrations with structure on large spatial scales subtracted. Note that the greyscale is different to Figure 3.2.

Models 1 and 2 are intended to represent the two extremes of negligible improvement and near-optimal improvement. A third model investigated for purposes of comparison was that of a diffraction-limited mirror. The three models are summarised in Table 3.1

Table 3.1: A brief summary of the three models used for the NOT mirror aberrations.

Model	Description of phase aberrations
1	as measured before adjustment of mirror supports
2	estimated aberrations after adjustment
3	a diffraction-limited mirror

For each of the models the telescope PSF in the absence of the atmosphere was generated using an FFT (as described in Chapter 1.2.2). The PSF Strehl ratios obtained were $0.23$, $0.87$ and $1.00$ for models 1, 2 and 3 respectively.

For the numerical simulations based upon these models, the secondary supports were ignored, and the telescope aperture was modelled as an annulus with inner radius $r_{s}$ equal to that of the secondary obscuration, and outer radius $r_{p}$ determined by the radius of the primary mirror (as shown in Figure 3.4). The shape of the aperture used in the simulations can be described mathematically in terms of the throughput $\chi_{t}\left ( r \right )$ as a function of radius $r$ (in the same way as for Equation 1.7):

$$\chi_{t}\left ( r \right ) = \left\{ \begin{array}{ll} 0 &... ...ft \vert \mathbf{r} \right \vert > r_{p}$} \end{array}\right.$$ (3.1)

For the NOT , $r_{p}=2.56$ $m$ and $r_{s}=0.70$ $m$.

Figure 3.4: The geometry of the NOT aperture

For each model, many realisations of atmospheric phase fluctuations that had a Kolmogorov distribution with $r_{0}$ seven times smaller than telescope diameter were calculated. These Kolmogorov distributions had a large outer scale (approximately thirty times the telescope diameter). The phase perturbations from the telescope mirror for each model were added to the simulated atmospheric phase distribution, and short exposure images were generated using the aperture shape described by Equation 3.1. The mirror aberrations in models $1$ and $2$ produce a reduction in the typical Strehl ratios for the short exposure images when compared with the diffraction-limited case. Histograms showing the frequency distribution of Strehl ratios measured for the short exposures from each of the models are shown in Figure 3.5.

Figure 3.5: Histograms of the Strehl ratios obtained in simulated short exposure images using each of the three models for the NOT mirror aberrations. Incoming wavefronts were simulated with a Kolmogorov spectrum of phase fluctuations, with coherence length $r_{0}$ seven times smaller than the telescope aperture diameter. The aperture geometry shown in Figure 3.4 was used for the simulations. Curve A corresponds to model 1, using the mirror aberrations measured by Andersen & Sørensen (1996); Sørensen (2002). Curve B corresponds to model 2, where the large scale fluctuations have been subtracted. Curve C corresponds to the case of a diffraction-limited telescope with the same aperture geometry.

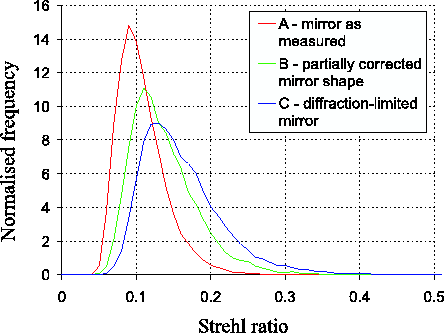It is interesting to note that with model $1$ (the worst-case scenario) some of the short exposures through the atmosphere have higher Strehl ratios than would be obtained in the absence of the atmosphere. In these exposures the atmospheric phase perturbations are compensating for the errors in the figure of the telescope mirror. This effect is even more noticeable under slightly better astronomical seeing conditions. One example of an exposure with very high Strehl ratio which appeared by chance in such a simulation is shown in Figures 3.6a--f. $r_{0}$ for this simulation was five times smaller than the telescope diameter. Figure 3.6a shows the selected exposure with a Strehl ratio of 0.32. The PSF of the telescope (in the absence of atmospheric perturbations) is shown in Figure 3.6b, with a Strehl ratio of 0.23. Figure 3.6c shows the PSF that would be obtained through the same atmosphere using a diffraction-limited telescope (i.e. the PSF for the atmospheric perturbations alone). The shape of this PSF is almost a mirror-image of Figure 3.6b, suggesting that the wavefront errors from the atmosphere are approximately equal and opposite to the aberrations introduced by the telescope. This is also apparent in Figures 3.6d, 3.6e and 3.6f which show greyscale maps of the wavefront error for the PSFs in Figures 3.6a, 3.6b and 3.6c respectively.

Figure 3.6: Atmospheric correction of the shape of the NOT mirror: a) shows a selected exposure; b) shows the PSF of the telescope; and c) shows the PSF for a diffraction limited telescope through the same atmosphere as in a). The compensation of the telescope aberrations by the atmosphere can also be seen in the wavefront error maps plotted as greyscale in d), e) and f), and corresponding to the PSF s shown in a), b) and c) respectively.

The atmosphere is much less likely to correct those phase perturbations which have small spatial scales across the telescope mirror, because the Kolmogorov wavefront perturbations have very little power on small spatial scales. The perturbations in model $2$ are restricted to small spatial scales so little correction is expected, but the phase perturbations in the model are sufficiently small in amplitude that they only have a small impact on the distribution of the measured Strehl ratios, as shown in Figure 3.5.

It is clear from the tails of the distributions in Figure 3.5 that we can expect the best short exposure images taken at the NOT to have reasonably high Strehl ratios under good atmospheric seeing conditions. Even with model 1, representing something of a worst-case scenario, Strehl ratios higher than $0.22$ are expected $1\%$ of the time.