Exposure selection

The phase perturbations introduced by the atmosphere change on timescales of a few milliseconds, causing the speckle patterns in Figures 1.3a and 1.3b to vary randomly in both shape and overall position (the changes in the position of the PSF correspond to the image-motion commonly known to observational astronomers). For the small aperture shown in Figure 1.3c the overall position of the PSF still fluctuates with time, but the shape of the short exposure PSF changes very little. The most prominent effects of atmospheric phase perturbations on the shape in this case are small fluctuations in the Airy rings and in the intensity of the central peak.

It is useful at this stage to define a quantitive measure of image quality. One approach is to compare the PSF measured through the atmosphere with the diffraction-limited PSF expected in the absence of atmospheric aberrations. The ratio of the peak intensity in the PSF measured for an aberrated optical system to that expected for a diffraction-limited system is widely known as the Strehl ratio, after the work of Strehl (1895,1902). In this case we treat the atmospheric perturbations as the optical aberration, with the telescope itself assumed to be aberration-free. In order to ensure that the images shown in Figure 1.3 were ``typical'', several thousand random realisations of each PSF were generated, and the three with the median Strehl ratios were chosen for the figure. The Strehl ratios of the exposures picked were $0.024$, $0.14$ and $0.68$ for Figures 1.3a, 1.3b and 1.3c respectively.

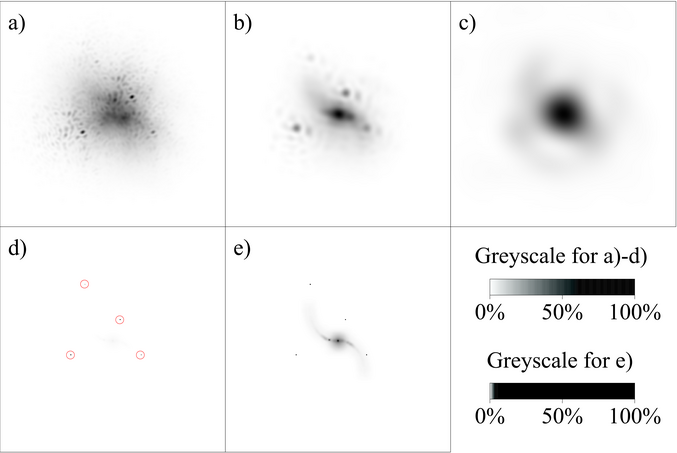
As the atmospheric fluctuations are random, one would occasionally expect these fluctuations to be arranged in such a way as to produce a diffraction-limited PSF, and hence good quality image. Fried (1978) coined the phrase ``Lucky Exposures'' to describe high quality short exposures which occur in such a fortuitous way. A perfectly diffraction-limited PSF will be extremely unlikely, but it is of interest to assess how good an image one would expect to occur relatively often during an observing run. If the speckle patterns change on timescales of a few milliseconds, and we are willing to wait a few seconds for our good image, then we can wait for a one-in-a-thousand Lucky Exposures. From several thousand random realisations I selected the PSFs with the highest 0.1% of Strehl ratios. Figures 1.4a--c show examples of these PSFs with the same atmospheric conditions and telescope diameters as were used for Figure 1.3a--c respectively.

Figure 1.4: Short exposures through a 20r0, 7r0 and 2r0 aperture typical of those with the highest 0.1% of Strehl ratios. The Strehl ratios for a), b) and c) are 0.0619, 0.426 and 0.905 respectively.

Figure 1.4a has one speckle with unusually high intensity, resulting in an image Strehl ratio of $0.062$ - significantly greater than the median Strehl of $0.024$ for short exposure PSFs with this aperture size. If the brightest speckle is similar in shape to a diffraction-limited PSF, then the fraction of the light in the brightest speckle is approximately equal to the Strehl ratio. In this case roughly $6\%$ of the light resides in the brightest speckle. The vast majority of the light is distributed in a large number of fainter speckles. When imaging a complex source, each of the fainter speckles contributes noise to the image, resulting in poor image quality.

Figure 1.4b is dominated by a single speckle which contains a significant fraction of the total intensity in the image. If we take this speckle to be similar in size and shape to a diffraction-limited PSF, then the measured Strehl ratio of 43% implies that the speckle contains about 43% of the total light intensity. The remaining light is found in a large number of much fainter speckles. The surface brightness from these background speckles is relatively small and should not result in a very noisy image.

Figure 1.4c is very similar to the typical exposure shown in Figure 1.3c. With this aperture size the PSF of a lucky exposure shows little improvement over that for a typical exposure. The broad core of the PSF is dominated by diffraction through the small aperture, giving very poor angular resolution.

Fried (1978) suggested that for an aperture of diameter $7r_{0}$ or $8r_{0}$, roughly 0.1% of the short exposures should be of very good quality (with the RMS variation in wavefront phase over the aperture less than one radian). This is borne out by the compact core and high Strehl ratio for the PSF shown in Figure 1.4b, which should mean that this case provides better high-resolution imaging performance than Figures 1.4a and 1.4c.

In order to compare the imaging performance of the PSFs qualitatively, each of the PSFs in Figures 1.4a--c was convolved with a simulated astronomical image; the results are shown in Figures 1.5a--c respectively. For comparison, an image on the same scale was generated using an ideal PSF (a delta-function), and this is displayed in Figures 1.5d and 1.5e. Both the galaxy-like structure and the point sources are clearly evident in Figure 1.5b, whereas these structures are much more difficult to make out in Figures 1.5a and 1.5c.

Figure 1.5: a)--c) show the short exposure PSF s from Figure 1.4 convolved with a simulated sky brightness distribution. The sky brightness distribution used is shown with two different greyscales in d) and e). Four point sources of differing brightness are circled in red in d). In panels a)--c) the blurring effect of the PSF s re-distributes the flux from the point sources over a wider area of the image leading to a substantial reduction in the peak pixel values in the images.

Even under high light level conditions the signal to noise for imaging using short exposures can be improved by combining large numbers of short exposures taken at different times. For PSFs having a bright core such as Figure 1.4b, the location of this core within the image is randomly determined by the atmosphere. To maximise the image quality, the images must be shifted so that the contribution from the bright core of each PSF is brought to a common location. If the short exposures are then co-added, the contribution from the bright core of each PSF will add coherently, while the contributions from the randomly varying speckles will combine incoherently. In practice the PSF must be determined from the short exposure images themselves - this is most easily achieved if there is an unresolved star within the field of view. The image of such a star obtained through the atmosphere accurately maps the PSF due to the telescope and atmosphere. The re-centring and co-adding of short exposures in this way has been widely discussed by other authors (e.g. Christou (1991)).

Determination of the instantaneous PSF from short exposure images of a reference star, and the use of such PSF measurements to select the exposures with the highest Strehl ratio and to then re-centre and co-add these exposures forms the basis for most of the work described in this thesis. I will refer to this method as the Lucky Exposures technique. A number of other authors have published results using very similar methods, particularly for solar and planetary observations. Observations of fainter astronomical targets have typically used exposure times which are too long to freeze the atmosphere, but these have often produced valuable astronomical science results nevertheless (Nieto & Thouvenot, 1991; Lelievre et al. , 1988; Nieto et al. , 1987,1988; Crampton et al. , 1989; Nieto et al. , 1990). Dramatic improvements in CCD technology have allowed recent observations to be performed at much higher frame rates (Dantowitz et al. , 2000; Davis & North, 2001; Baldwin et al. , 2001), providing new insights into the characteristics of the atmosphere, and demonstrating the potential of high frame-rate imaging using low noise detectors.

To help provide some background material in the field of high resolution imaging, I will now introduce some alternative methods for high resolution imaging. This will hopefully clarify the advantages and disadvantages of Lucky Exposures.