Limiting magnitude of reference source for adaptive optics

Active correction of wavefront perturbations introduced by the atmosphere is known as adaptive optics. The simplest form of adaptive optics system is a mechanical tip-tilt corrector which removes the average gradient in wavefront phase across a telescope aperture. With this level of correction, diffraction-limited long exposure imaging can only be performed for aperture diameters up to 3.4$r_{0}$ diameter (Noll, 1976). To obtain diffraction-limited images from larger telescopes, the shape of the perturbations in the wavefront across the telescope aperture must be measured and actively corrected. Deformable mirrors in a re-imaged pupil-plane are most often used to introduce additional optical path which corrects the perturbations introduced by the atmosphere as shown schematically in Figure 1.8. One of the simplest systems for measuring the shape of the wavefront is a Shack-Hartmann array (see Figure 1.9). 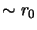This consists of a series of subapertures typically of $\sim r_{0}$ diameter, positioned across a telescope pupil-plane. The wavefront sensor accepts light from the reference star, while light from the science object (or light at a science imaging wavelength) is directed to a separate imaging camera. Each subaperture contains a focusing element which generates an image of the reference source, and the position offset of these images is used to calculate the mean gradient of the wavefront phase over each subaperture. The gradient measurements can then be pieced together to provide a model for the shape of the wavefront perturbations. This model is then fed into the wavefront corrector. In order to accurately correct the rapidly fluctuating atmosphere using a stable servo-feedback loop, the process must typically be repeated ten times per atmospheric coherence time (see e.g. Hardy (1998); Karr (1991)). The atmospheric coherence time itself is usually found to be shorter for measurements through small subapertures than for imaging through the full telescope aperture, as will be discussed further in Chapter 2 (see also Roddier et al. (1982a)).

Figure 1.8: Adaptive optics correction of atmospherically perturbed wavefronts using a deformable mirror.

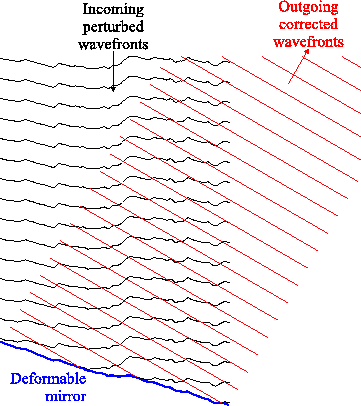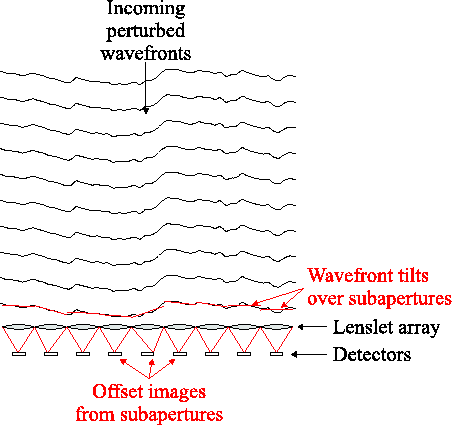
Figure 1.9: Schematic of a Shack-Hartmann wavefront sensor positioned in a telescope pupil-plane. An array of lenslets act as subapertures, and the position of the image centroid measured using each subaperture is used to calculate the wavefront tilt over this subaperture. These wavefront tilts are then used to construct a model of the wavefront shape over the full telescope aperture.