Numerical simulations
A number of numerical simulations were undertaken to investigate the
temporal properties of Taylor screen models more
rigorously. Initially, two models were investigated, the first with a
single Taylor screen moving at a constant wind speed as discussed in
Chapter 2.3.2, the second having two equal Taylor
screens with slightly different wind speeds but the same wind
direction. The properties of the two models are summarised in
Table 2.1. The Taylor phase screens used had
Kolmogorov turbulence extending to an outer scale of 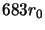 , with
no power on spatial frequencies larger than this. The size of the
outer scale was determined by the available computer memory. Both
simulations produced wavefront perturbations with the same coherence
length
, with
no power on spatial frequencies larger than this. The size of the
outer scale was determined by the available computer memory. Both
simulations produced wavefront perturbations with the same coherence
length  . Images from filled circular apertures with diameters
between
. Images from filled circular apertures with diameters
between 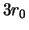 and
and 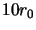 were generated at a large number of
discrete time points.
were generated at a large number of
discrete time points.
Table 2.1:
A brief summary of the two model atmospheres
investigated. The third column shows the scatter in the wind
velocities calculated using Equation 2.10.
|
|
Photometric measurements were made at a fixed point in the image plane
corresponding to each of the simulated apertures at each time point,
and the temporal autocorrelation of this data was
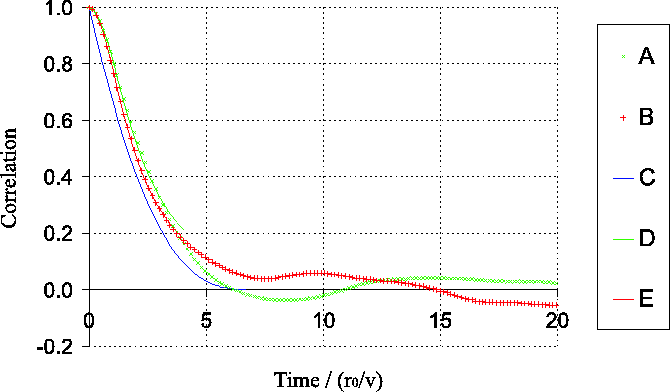
calculated. Figure 2.4 shows two example
autocorrelations for an aperture diameter of 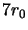 . There is
relatively good agreement between the model of Aime et al. (1986)
(Equation 2.2) and the normalised
autocorrelation data from numerical simulations up to time differences
corresponding to the coherence timescale
. There is
relatively good agreement between the model of Aime et al. (1986)
(Equation 2.2) and the normalised
autocorrelation data from numerical simulations up to time differences
corresponding to the coherence timescale 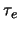 . For larger time
differences Equation 2.2 tends quickly to
zero, while the simulation data usually drifted either side of zero
somewhat. This may be due to the limited timescale of the simulations
(a few hundred times
. For larger time
differences Equation 2.2 tends quickly to
zero, while the simulation data usually drifted either side of zero
somewhat. This may be due to the limited timescale of the simulations
(a few hundred times 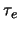 , which is not long enough to average
very many realisations of the longer timescale changes in the speckle
pattern). Similar results were found for all of the aperture diameters
simulated, and the temporal power spectra were found to agree with the
model of Aime et al. (1986).
, which is not long enough to average
very many realisations of the longer timescale changes in the speckle
pattern). Similar results were found for all of the aperture diameters
simulated, and the temporal power spectra were found to agree with the
model of Aime et al. (1986).
Figure 2.4:
Two examples of the temporal autocorrelation curves generated from
numerical simulations (and used to produce
Figure 2.5). The curves have been normalised using the
method described in Chapter 2.2.1. A
shows the result for a single layer atmosphere and B for a
two-layer atmosphere (models 1 and 2 from
Table 2.1 respectively). C shows the
predicted decorrelation using the highly simplified model for a single
layer atmosphere described in
Appendix A. D and
E show least-squared fits of the form of
Equation 2.2 to the early parts of
curves A and B respectively.
 |
The coherence
timescale 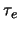 was then calculated from each simulation using
the method described in Chapter 2.2.1. A plot of
the variation of the coherence timescale with telescope aperture
diameter is shown in Figure 2.5.
was then calculated from each simulation using
the method described in Chapter 2.2.1. A plot of
the variation of the coherence timescale with telescope aperture
diameter is shown in Figure 2.5.
Figure 2.5:
Timescale 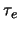 for a range of aperture diameters, for the two
atmospheric models. Curve A shows the result for a single
Taylor screen of frozen Kolmogorov turbulence. B is a similar
plot for the two layer atmosphere listed as model 2 in
Table 2.1. The error bars simply indicate the
standard error of the mean calculated from the scatter in results from
a number of repeated Monte Carlo simulations. Errors in the
measurements at different aperture diameters are partially correlated
as the same realisations of the model atmospheres were used for all
the aperture diameters shown. The red line is described by
Equation 2.14 and the black horizontal line is at
the value given in Equation 2.15.
for a range of aperture diameters, for the two
atmospheric models. Curve A shows the result for a single
Taylor screen of frozen Kolmogorov turbulence. B is a similar
plot for the two layer atmosphere listed as model 2 in
Table 2.1. The error bars simply indicate the
standard error of the mean calculated from the scatter in results from
a number of repeated Monte Carlo simulations. Errors in the
measurements at different aperture diameters are partially correlated
as the same realisations of the model atmospheres were used for all
the aperture diameters shown. The red line is described by
Equation 2.14 and the black horizontal line is at
the value given in Equation 2.15.
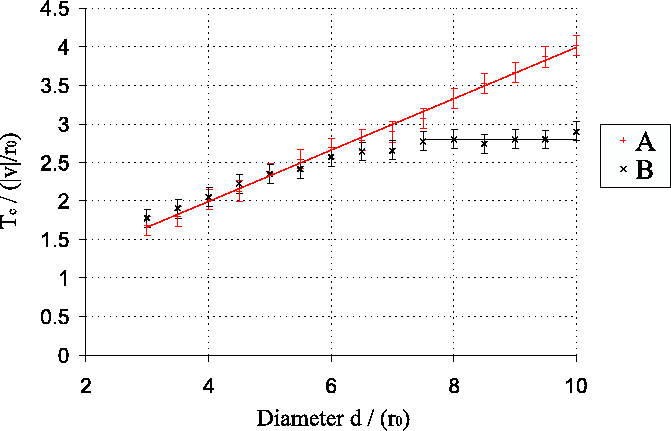 |
The red line in Figure 2.5 is a linear regression fit
to the measured timescale 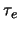 for simulations with a single
Taylor screen. The equation for this best fit line is:
for simulations with a single
Taylor screen. The equation for this best fit line is:
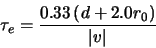 |
(2.14) |
The timescale appears to depend approximately linearly on the aperture
diameter 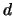 , as predicted in
Appendix A. The value of
, as predicted in
Appendix A. The value of 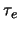 was
found to be larger than predicted by my simplified model by a constant
amount
was
found to be larger than predicted by my simplified model by a constant
amount
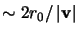 . This is consistent
with a small region of the atmospheric layers extending
. This is consistent
with a small region of the atmospheric layers extending 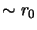 into areas
into areas 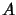 and
and 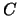 in Figure A.3 being correlated
with the phase perturbations in area
in Figure A.3 being correlated
with the phase perturbations in area 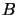 . The same hypothesis would
explain why the measured temporal autocorrelations shown in
Figure 2.4 as curves A and B lie to
the right of the prediction corresponding to my simplified model
(curve C) over the left-hand part of the graph.
. The same hypothesis would
explain why the measured temporal autocorrelations shown in
Figure 2.4 as curves A and B lie to
the right of the prediction corresponding to my simplified model
(curve C) over the left-hand part of the graph.
For small aperture diameters, the simulations with a two-layer
atmosphere have very similar timescales to those with a single
atmospheric layer. However there is a knee at
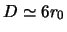 , and at
diameters larger than this the timescale
, and at
diameters larger than this the timescale 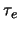 appears to be
constant at:
appears to be
constant at:
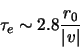 |
(2.15) |
where
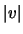 is the average wind velocity for the two
layers. It is of interest to compare this timescale with that
predicted by Equations 2.11 and
2.12. For this atmospheric model, the wind scatter
is the average wind velocity for the two
layers. It is of interest to compare this timescale with that
predicted by Equations 2.11 and
2.12. For this atmospheric model, the wind scatter
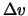 is equal to:
is equal to:
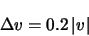 |
(2.16) |
The timescale 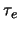 can be written in terms of
can be written in terms of  :
:
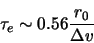 |
(2.17) |
This is larger than the timescales predicted by both
Equation 2.11 (from Roddier et al. (1982a)) and
Equation 2.12 (from Aime et al. (1986)). The result of
Aime et al. (1986) is within 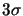 of these simulations however
(remembering that the errors in the simulations are correlated for
different aperture diameters).
of these simulations however
(remembering that the errors in the simulations are correlated for
different aperture diameters).
Figure 2.5 implies that the timescale for changes in
the speckle pattern found at the focus of a well figured astronomical
telescope may increase somewhat with aperture diameter if the
atmospheric turbulence is moving with a common wind velocity. This would
not be the case if there is a substantial scatter in the wind
velocities, as the timescale saturates at a level close to that
predicted by Equation 2.12. Vernin & Muñoz-Tuñón (1994) found
that the scatter in the velocities of the turbulent layers above the
NOT is small enough that the timescale for speckle patterns using the
full aperture of the NOT should be twice the timescale which would be
found with small apertures, or that for standard adaptive optics
correction. This is consistent with measurements by
Saint-Jacques & Baldwin (2000) which indicated that a single wind velocity (or
narrow range of wind velocities) dominates above La Palma. This
contrasts with results at a number of other observatories
(e.g. Parry et al. (1979); Vernin & Roddier (1973); Caccia et al. (1987); Roddier et al. (1993)) where either strong
turbulence is found in several layers with differing wind velocities,
or there is little evidence for any bulk motion of the atmospheric
perturbations across the telescope aperture. Wilson (2003) also
found evidence for significant dispersion in the wind velocities above
the WHT on some nights.
Bob Tubbs
2003-11-14
![]() . There is
relatively good agreement between the model of Aime et al. (1986)
(Equation 2.2) and the normalised
autocorrelation data from numerical simulations up to time differences
corresponding to the coherence timescale
. There is
relatively good agreement between the model of Aime et al. (1986)
(Equation 2.2) and the normalised
autocorrelation data from numerical simulations up to time differences
corresponding to the coherence timescale ![]() . For larger time
differences Equation 2.2 tends quickly to
zero, while the simulation data usually drifted either side of zero
somewhat. This may be due to the limited timescale of the simulations
(a few hundred times
. For larger time
differences Equation 2.2 tends quickly to
zero, while the simulation data usually drifted either side of zero
somewhat. This may be due to the limited timescale of the simulations
(a few hundred times ![]() , which is not long enough to average
very many realisations of the longer timescale changes in the speckle
pattern). Similar results were found for all of the aperture diameters
simulated, and the temporal power spectra were found to agree with the
model of Aime et al. (1986).
, which is not long enough to average
very many realisations of the longer timescale changes in the speckle
pattern). Similar results were found for all of the aperture diameters
simulated, and the temporal power spectra were found to agree with the
model of Aime et al. (1986).

![]() was then calculated from each simulation using
the method described in Chapter 2.2.1. A plot of
the variation of the coherence timescale with telescope aperture
diameter is shown in Figure 2.5.
was then calculated from each simulation using
the method described in Chapter 2.2.1. A plot of
the variation of the coherence timescale with telescope aperture
diameter is shown in Figure 2.5.

![]() for simulations with a single
Taylor screen. The equation for this best fit line is:
for simulations with a single
Taylor screen. The equation for this best fit line is:
![]() , and at
diameters larger than this the timescale
, and at
diameters larger than this the timescale ![]() appears to be
constant at:
appears to be
constant at: