In order to assess the imaging performance of the Strehl selection
method, the data on V656 Herculis and 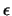 Aquilae listed in
Table 3.2 were analysed using the approach described in
Figure 3.13. The best
Aquilae listed in
Table 3.2 were analysed using the approach described in
Figure 3.13. The best 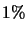 of exposures were selected
and co-added - the resulting images for V656 Herculis and
of exposures were selected
and co-added - the resulting images for V656 Herculis and 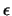 Aquilae are shown in Figures 3.14a and
3.14b. Shown beneath are the average (seeing-limited)
images from the same data in Figures 3.14c and
3.14d, representing conventional long exposures. It is
possible that telescope tracking errors might have contributed to the
asymmetry in the long exposure image of V656 Herculis, but it is
difficult to distinguish these errors from the random motion due to
the atmosphere.
Aquilae are shown in Figures 3.14a and
3.14b. Shown beneath are the average (seeing-limited)
images from the same data in Figures 3.14c and
3.14d, representing conventional long exposures. It is
possible that telescope tracking errors might have contributed to the
asymmetry in the long exposure image of V656 Herculis, but it is
difficult to distinguish these errors from the random motion due to
the atmosphere.
The image selection method provides images with FWHM of 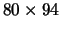
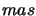 for V656 Herculis and
for V656 Herculis and 
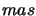 for
for 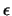 Aquilae,
a very substantial improvement over the FWHM of the conventional
astronomical images (
Aquilae,
a very substantial improvement over the FWHM of the conventional
astronomical images (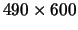
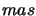 and
and 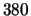
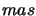 respectively). In the Lucky Exposures images the first Airy ring is visible
(although it is not uniform around the stars). In both images the total
flux beyond the first Airy ring is relatively small. If these PSF
were available for imaging complex fields, extremely high image
resolution and quality would be obtained.
respectively). In the Lucky Exposures images the first Airy ring is visible
(although it is not uniform around the stars). In both images the total
flux beyond the first Airy ring is relatively small. If these PSF
were available for imaging complex fields, extremely high image
resolution and quality would be obtained.
Figure 3.14:
Two stars were observed on the first night at the NOT without
saturation - V656 Herculis and 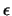 Aquilae. Panels a)
and b) show the best 1% of exposures shifted and added for
V656 Herculis and
Aquilae. Panels a)
and b) show the best 1% of exposures shifted and added for
V656 Herculis and 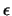 Aquilae respectively, processed using the
method described in the text. Beneath these panels are the respective
averaged images in panels c) and d). These were
generated by summing all of the short exposures without re-centring,
and represent the conventional astronomical seeing disks at the times
of the observations. The Strehl ratios and FWHM for the four images
are: a)
Aquilae respectively, processed using the
method described in the text. Beneath these panels are the respective
averaged images in panels c) and d). These were
generated by summing all of the short exposures without re-centring,
and represent the conventional astronomical seeing disks at the times
of the observations. The Strehl ratios and FWHM for the four images
are: a) 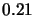 and
and 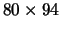
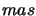 , b)
, b) 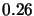 and
and
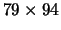
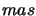 , c)
, c) 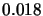 and
and 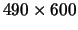
 ,
d)
,
d) 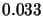 and
and 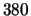
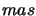 .
.
 |
Bob Tubbs
2003-11-14
![]()
![]() for V656 Herculis and
for V656 Herculis and ![]()
![]() for
for ![]() Aquilae,
a very substantial improvement over the FWHM of the conventional
astronomical images (
Aquilae,
a very substantial improvement over the FWHM of the conventional
astronomical images (![]()
![]() and
and ![]()
![]() respectively). In the Lucky Exposures images the first Airy ring is visible
(although it is not uniform around the stars). In both images the total
flux beyond the first Airy ring is relatively small. If these PSF
were available for imaging complex fields, extremely high image
resolution and quality would be obtained.
respectively). In the Lucky Exposures images the first Airy ring is visible
(although it is not uniform around the stars). In both images the total
flux beyond the first Airy ring is relatively small. If these PSF
were available for imaging complex fields, extremely high image
resolution and quality would be obtained.
