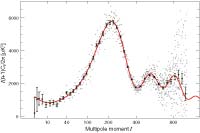
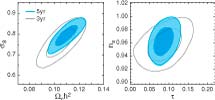
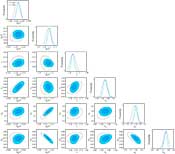
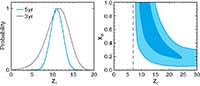
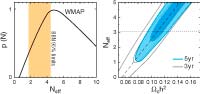
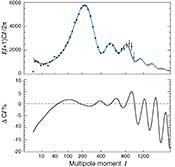
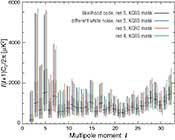
Likelihoods and Parameters

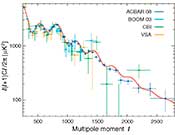
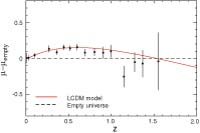
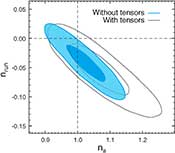
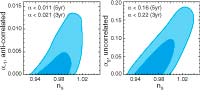
Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Likelihoods and Parameters from WMAP Data, J. Dunkley, et al., 2009ApJS..180..306D, reprint / preprint (1.2 MB) / bundled figures (312 KB) / individual figures / ADS / astro-ph

WMAP Five-year Paper Figures, J. Dunkley, et al.
Individual figures are provided for use in talks. Proper display of PNG transparency in PowerPoint requires saving files to your computer before Inserting them. Please acknowledge the WMAP Science Team when using these images. Image Credit: NASA / WMAPScience Team
	Fig. 1 This figure compares the low-l TT power spectrum computed with two different techniques. At each l value, we plot the maximum likelihood value (tic mark), the region where the likelihood is greater than 50% of the peak value (thick line) and the region where the likelihood is greater than 95% of the peak value (thin line). The black lines (left side of each pair) are estimated by Gibbs sampling using the ILC map smoothed with a 5 degree Gaussian beam (at HEALPix Nside = 32). The light blue line (right side of the pair) is estimated with a pixel-based likelihood code with Nside = 16. The slight differences between the points are primarily due to differences in resolution. At each multipole, the likelihood is sampled by fxing the other Cl values at a fiducial spectrum (red).	PNG (9 kb - 1024x817 pixels) PNG (22 kb - 1633x2048 pixels) EPS (38 kb)
	Fig. 2 The temperature angular power spectrum corresponding to the WMAP-only best-fit ΛCDM model. The grey dots are the unbinned data; the black data points are binned data with 1σ error bars including both noise and cosmic variance computed for the best-fit model.	PNG (13 kb - 1024x679 pixels) PNG (29 kb - 1358x2048 pixels) EPS (104 kb)
	Fig. 3 Constraints on ΛCDM parameters from the five-year WMAP data. The two-dimensional 68% and 95% marginalized limits are shown in blue. They are consistent with the three-year constraints (grey). Tighter limits on the amplitude of matter fluctuations, σ8, and the cold dark matter density Ωch2, arise from a better measurement of the third temperature (TT) acoustic peak. The improved measurement of the EE spectrum provides a 5σ detection of the optical depth to reionization, Τ , which is now almost uncorrelated with the spectral index ns.	PNG (10 kb - 1024x475 pixels) PNG (23 kb - 951x2048 pixels) EPS (60 kb)
	Fig. 4 Constraints from the five-year WMAP data on ΛCDM parameters (blue), showing marginalized one-dimensional distributions and two-dimensional 68% and 95% limits. Parameters are consistent with the three-year limits (grey) from Spergel et al. (2007), and are now better constrained.	PNG (56 kb - 2048x1800 pixels) PNG (135 kb - 3600x4096 pixels) EPS (338 kb)
	Fig. 5 Left: marginalized probability distribution for zreion in the standard model with instantaneous reionization. Sudden reionization at z = 6 is ruled out at 3.5s, suggesting that reionization was a gradual process. Right: in a model with two steps of reionization (with ionization fraction xe at redshift zr, followed by full ionization at z = 7), the WMAP data are consistent with an extended reionization process.	PNG (8 kb - 439 x1024 pixels) PNG (18 kb 878x2048 pixels) EPS (25 kb)
	Fig. 6 Effect of foreground treatment and likelihood details on ΛCDM parameters. Left: The number of bands used in the template cleaning (denoted `T'), affects the precision to which τ is determined, with the standard KaQV compared to QV and KaQVW, but has little effect on other cosmological parameters. Using maps cleaned by Gibbs sampling (KKaQV (G)) also gives consistent results. Right: Lowering the residual point source contribution (`lower ptsrc') and removing the marginalization over an SZ contribution (`No SZ') affects parameters by < 0.4σ. Using a larger mask (`80% mask') has a greater effect, increasing Ωbh2 by 0.5σ, but is consistent with the effects of noise.	PNG (37 kb - 1048x2048 pixels) PNG (90 kb 2096x4096 pixels) EPS (114 kb)
	Fig. 7 Best-fit temperature angular power spectrum from WMAP alone (red), which is consistent with data from recent small-scale CMB experiments: ACBAR, CBI, VSA, and BOOMERANG.	PNG (11 kb - 1024x788 pixels) PNG (27 kb - 1576x2048 pixels) EPS (40 kb)
	Fig. 8 Baryon Acoustic Oscillations expected for the best-fit ΛCDM model (red lines), compared to BAO in galaxy power spectra calculated from (left) combined SDSS and 2dFGRS main galaxies, and (right) SDSS LRG galaxies, by Percival et al. (2007a). The observed and model power spectra have been divided by P(k)smooth, a smooth cubic spline fit described in Percival et al. (2007a).	PNG (17 kb - 2048x731 pixels) PNG (41 kb - 1463x4096 pixels) EPS (25 kb)
	Fig. 9 Red line shows the luminosity distance relationship predicted for the best-fit WMAP-onlymodel (the right column in Table 2). The points show binned supernova observations from the Union compilation (Kowalski et al. 2008), including high-redshift SNIa from Hubble Space Telescope (HST; Riess et al. 2007), ESSENCE (Miknaitis et al. 2007), and SNLS (Astier et al. 2006). The plot shows the deviation of the luminosity distances from the empty universe model.	PNG (6 kb - 683x1024 pixels) PNG (15 kb - 1365x2048 pixels) EPS (20 kb)
	Fig. 10 Two-dimensional marginalized constraints (68% and 95% confidence levels) on inflationary parameters r, the tensor-to-scalar ratio, and ns, the spectral index of fluctuations, defined at k0 = 0.002/Mpc. One-dimensional 95% upper limits on r are given in the legend. Left: the five-year WMAP data place stronger limits on r (shown in blue) than three-year data (gray). This excludes some inflationary models including λφ4 monomial inflaton models with r ~ 0.27, ns ~ 0.95 for 60 e-folds of inflation. Right: for models with a possible running spectral index, r is now more tightly constrained due to measurements of the third acoustic peak. Note: the two-dimensional 95% limits correspond to Δ(2 ln L) ~ 6, so the curves intersect the r = 0 line at the ~ 2.5s limits of the marginalized ns distribution.	PNG (22 kb - 427x1024 pixels) PNG (24 kb - 853x2048 pixels) EPS (47 kb)
	Fig. 11 Two-dimensional marginalized limits for the spectral index, ns, defined at k0 = 0.002/Mpc, and the running of the index dns/dln k (marked nrun). Models with no tensor contribution, and with a tensor contribution marginalized over, are shown. In both cases the models are consistent with a power-law spectral index, with dns/dln k = 0, as expected from the simplest in inflationary models.	PNG (11 kb - 898x1028 pixels) PNG (26 kb - 1796x2056 pixels) EPS (31 kb)
	Fig. 12 Marginalized two-dimensional limits (68% and 95%) on the amplitude of possible CDM entropy (or isocurvature) fluctuations. The one-dimensional 95% upper limits are given in the legend. Left: Anticorrelated fluctuations are tightly constrained, placing limits on curvaton models. Right: Uncorrelated fluctuations, corresponding to axion models for dark matter, add less power to the CMB spectrum than the anti-correlated case, for a given α. In both cases the amplitude is correlated with the spectral index of curvature fluctuations ns, which compensates for the large scale power added by the CDM entropy fluctuations.	PNG (9 kb - 492x1024 pixels) PNG (21 kb - 983x2040 pixels) EPS (47 kb)
	Fig. 13 Evidence for a non-zero effective number of neutrino species, Neff. Left: The marginalized probability distribution gives Neff > 2.3 (95% CL) from WMAP alone. The best-fit ΛCDM model with Neff = 0 is a poorer fit to the data than Neff = 3, with ΔX2 = 8.2. Right: Joint two-dimensional distribution for Neff and the CDM density, Ωch2, with five-year limits in blue, compared to three-year limits in grey. The degeneracy valley of constant zeq is shown dashed, indicating that the CMB is now sensitive to the effect of neutrino anisotropic stress, which breaks the degeneracy.	PNG (10 kb - 479x1024 pixels) PNG (44 kb - 959x2048 pixels) EPS (36 kb)
	Fig. 14 Comparison of the CMB angular power spectrum for the best-fit ΛCDM models with the standard Neff = 3.04 neutrino species (red), and with Neff = 0 species (blue). Bottom: The fractional difference between the two spectra when Neff is increased from 0 to 3.04. The Neff = 0 model has a lower Ωmh2 in order to fit the third peak, and a lower spectral index, ns, compared to the Neff = 3.04 model.	PNG (13 kb - 979x1028 pixels) PNG (30 kb - 1958x2048 pixels) EPS (38 kb)
	Fig. 15 Limits on the sum of neutrino masses with the WMAP five-year data. Left: The marginalized one-dimensional limit from WMAP alone is Σmv < 1.3 eV (95% CL). This is raised by <10% with marginalization over a running spectral index, tensor fluctuations, or a dark energy equation of state w. Right: The neutrino mass is anti-correlated with σ8, the amplitude of matter fluctuations.	PNG (10 kb - 471x1024 pixels) PNG (22 kb - 943x2048 pixels) EPS (35 kb)
	Fig. 16 Left: The points show the set of non-flat models consistent with the WMAP data, colored by the Hubble constant values. The value of -2 lnL for all points shown is within 16 of the best-fit value. WMAP measures the acoustic peak scale to high accuracy, but does not constrain the curvature, Ωk, by itself. However, the highly curved models have a low Hubble constant, inconsistent with observation. Right: Constraints on the dark energy equation of state, w, and the dark energy density, ΩΛ, from WMAP alone. With a Hubble constant H0 < 100, weak limits can be placed on w in a flat universe, shown by the blue contours, but the dark energy density and equation of state are unconstrained (with the 95% confidence level shaded grey) if the assumption of flatness is relaxed. Limits are significantly improved when WMAP is combined with additional data (Komatsu et al. 2009).	PNG (30 kb - 804x1812 pixels) PNG (69 kb - 1609x3625 pixels) EPS (465 kb)
	Fig. 17 The angular power spectra of signal and noise components in the smoothed ILC map used for Gibbs sampling the low-l temperature spectrum. Uncorrelated noise, at 2 μK per pixel (red), is added to the smoothed ILC map to speed up the sampling, and then is assumed to be the only noise present. This assumption is inaccurate at low l, as it ignores the true noise (blue), but the error is negligible since it is significantly lower than cosmic variance (green).	PNG (10 kb - 731x1024 pixels) PNG (22 kb - 1463x2048 pixels) EPS (44 kb)
	Fig. 18 The level of variation in the low-ell TT Gibbs likelihood that arises from different input parameters. The spectrum estimated from the standard input (black) is compared to results obtained using a different white noise realization (blue), using a larger mask (KQ80,red), and degrading to Nside = 16 (green) rather then 32. The likelihood does fluctuate with these changes, but has a negligible effect on cosmological parameters. The values shown at each multipole correspond to maximum likelihood values obtained by fixing the spectrum of other multipoles at fiducial values. The error bars show where the likelihood is at 50% and 5% of its peak value.	PNG (11 kb - 817x1024 pixels) PNG (27 kb - 1633x2048 pixels) EPS (61 kb)