WMAP Seven Year Anomalies Results Paper
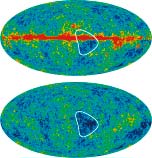
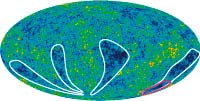
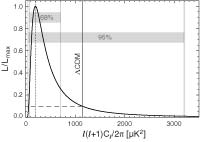
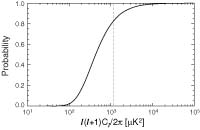
Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Are There Cosmic Microwave Background Anomalies?, Bennett, C., et.al., 2011ApJS..192...17B, reprint / preprint (999 KB) / bundled figures (926 KB) / individual figures / ADS / astro-ph
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||