

Matter DensityThe Ωm parameter specifies the mean present day fractional energy density of all forms of matter, including baryonic and dark matter. As can be seen in the figure below, a wide variety of techniques have been employed to determine Ωm. The diversity of techniques have not yet converged upon a tightly constrained concordance value, but recent estimates indicate only ∼30% of the total energy density in the universe is contributed by matter (see the gray vertical line in the figure). Galaxy surveys have been used to determine matter density in a variety of ways; we cite several examples. Many early visible light determinations depended on a mass-to-light ratio computed on large scales combined with an estimated luminosity density for the universe (Bahcall et al. 1995). Representative of this method is the CNOC sample, which used X-ray selected clusters of galaxies. Galaxy cluster abundances may be used for a determination of Ωm. However, these are sensitive to a combination of Ωm and σ8, thus requiring some method of breaking the degeneracy. Included in this category is the Planck 2013 analysis of their tSZ-selected sample of clusters, which employed external datasets to break the degeneracy imposed by the cluster constraints alone. This method is also discussed in the σ8 section. Weak lensing may alternatively be used to estimate the dark matter halo masses associated with visible galaxies, but this also carries similar parameter degeneracy difficulties. More et al. (2015) combined BOSS galaxy clustering data with the galaxy-galaxy lensing signal obtained from a spatially overlapping region in the CFHTLLenS catalog, in order to fit dark matter halo occupation model parameters and cosmological parameters. Although Ωm and σ8 are free parameters, priors were placed on other cosmological parameters using WMAP nine-year results. Estimates of the growth rate of structure ƒ from deep large-scale galaxy surveys may also be used to derive Ωm. As described in e.g. Nesseris & Perivolaropoulos (2008), ƒ = β b ≈ Ωm0.6, where b is the bias factor relating the distribution of mass in galaxies to the total matter distribution, and β is the redshift space distortion parameter derived from peculiar velocities. Verde et al. (2002) computed the bispectrum of 2dFGRS galaxies and used it to measure the bias parameter of the galaxies, then combined it with the 2dFGRS measurement of the redshift distortion parameter to yield Ωm at the effective redshift of the survey (z=0.17). A similar concept was used by da-Ângela et al.( 2008) on a QSO sample; their value of Ωm = 0.25 ± 0.08 is consistent with the Verde et al. (2002) result. The baryon acoustic oscillation feature seen in the correlation function of galaxies and Lyα absorbers may be modeled assuming a given cosmology and used to provide some parameter estimates which are independent of CMB determinations. Addison, Hinshaw & Halpern (2013) used combined BAO determinations in the range 0.1 < z < 2.4, coupled with large-scale structure clustering constaints (e.g. Alcock-Paczinski test) to determine values for Ωm and σ8. This analysis deliberately avoids the use of strong CMB priors in order to provide a more independent check on CMB-based results. Galaxy clustering methods may be avoided altogether through SNIa studies. Luminosity distances derived for a sample of SNIa may be used to directly constrain Ωm. under the assumption of ΛCDM cosmology (see e.g. Riess et al. 2004). We display the result of Riess et al. (2004), who used a combined sample of HST and ground-based SNIa observations to obtain Ωm = 0.29+0.05-0.03. Earlier values are in agreement, but with larger uncertainties, such as that from Steigman et al. (2000), (Ωm = 0.28 ± 0.08) utilizing data from SCP (Perlmutter et al. 1999) and HZT (Schmidt et al. 1998). Control of luminosity distance systematics is a recognized issue. Betoule et al. (2014) describe a joint recalibration of SNLS and SDSS SNIa samples with improvements in systematic uncertainties, leading to a derived value Ωm = 0.295 ± 0.034. The current most extensive SNIa compilation is the Pantheon sample (Scolnic et al. 2018), which includes Pan-STARRS1, SNLS, SDSS and HST observations which have been cross-calibrated to Pan-STARRS1. Including systematic uncertainties, Scolnic et al. find Ωm = 0.298 ± 0.022 for standard ΛCDM cosmology, providing the tightest uncertainty obtained from this method in the plot. Abbott et al. (2018) determine a value of 0.331 ± 0.038 from a smaller SNIa sample that includes independent Dark Energy Survey (DES) observations. 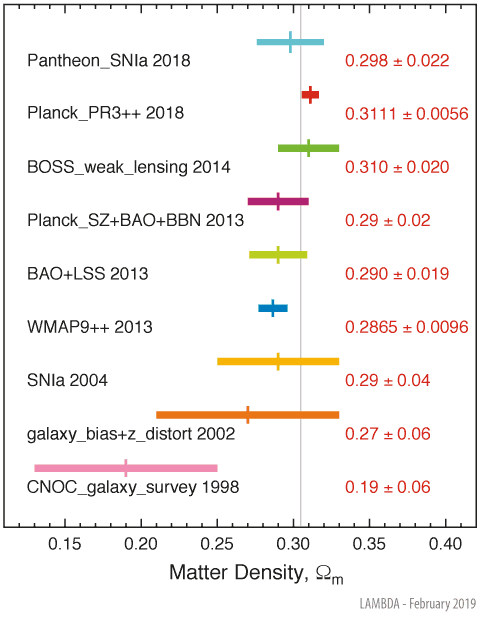 Image Credit: NASA / LAMBDA Archive Team Aside from CMB-related determinations, methods to determine total matter density include cosmological interpretation of galaxy cluster abundances, redshift-space distortion measurements, BAO and SNIa luminosity distances. A number of difficulties arise from parameter degeneracies involved in the galaxy clustering techniques. These may be avoided with SNIa analyses, but in this case control of luminosity distance determination systematics is a key factor and affects the quoted uncertainties. Ωm is one of the less well-determined parameters presented here: mild tension exists between the two CMB results quoting the smallest uncertainties (WMAP 2013 and Planck 2018), and constraints from non-CMB determinations are not yet sufficiently tight to highlight any coflicts with CMB results. The gray vertical line, representing the weighted average of WMAP and Planck data points, is positioned at Ωm = 0.3049.
Contributed by the NASA / LAMBDA Archive Team. |

