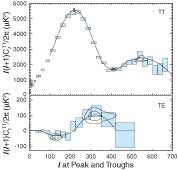
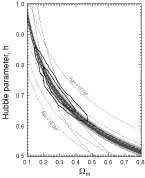
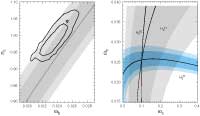
WMAP First Year Power Spectrum Peaks

First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Interpretation of the TT and TE Angular Power Spectrum Peaks, L. Page, et al., 2003ApJS..148..233P, reprint / preprint (288 Kb) / individual figures / ADS / astro-ph

WMAP First-year Paper Figures, L. Page, et al.
Individual figures are provided for use in talks. Proper display of PNG transparency in PowerPoint requires saving files to your computer before Inserting them. Please acknowledge the WMAP Science Team when using these images. Image Credit: NASA / WMAPScience Team
	Fig.1 Binned WMAP data are shown as boxes, the maximum likelihood peak model from the peak fitting functions is shown as the solid line, and the uncertainties are shown as closed contours. The top panel shows the TT angular power spectrum. The bottom panel shows the TE angular cross-power spectrum. For each peak or trough, the contours from the MCMC chains are multiplied by a uniform prior and so they are equal to contours of the a posteriori likelihood of the data given the model. The contours are drawn at Δχ2 = 2.3 and 6.18 corresponding to 1σ and 2σ.	PNG (34 kb - 2048x1966 pixels) PNG (84 kb - 4096x3932 pixels) EPS (26 kb)
	Fig.2 WMAP data in the Ωm-h plane. The thick solid contours in black are at Δχ2 = - 2.3, -6.18 (1σ, 2σ) of the marginalized likelihood from the full analysis (Spergel et al. 2003). The filled region is the constraint from the position of the first peak, with ωb = 0.023 fixed. In effect, it shows how Ωm and h must be related to match the observed position of the first peak in a flat geometry or, equivalently, to match the measured values of θA. The darker inner region corresponds to 1σ, and the lighter outer region corresponds to 2σ. The dotted lines are isochrons separated by 1 Gyr. It is clear that the WMAP data pick out 13.6 Gyr for the age of the universe in the flat, w = -1 case. The dashed lines show the 1σ limits on ωm. The light dashed line shows Ωmh3.4 = constant.	PNG (38 kb - 2048x1669 pixels) PNG (88 kb - 4096x3339 pixels) EPS (31 kb)
	Fig.3 Left: Parameter restrictions from H2TT in the ωb - ns plane. The gray swath is the 1&sigma band corresponding to H2TT = 0.426 ± 0.015 with ωm = 0.14. The swath is broadened if one includes the uncertainty in ωm. The light gray swath is 2σ. The solid line in the middle of the swath is for ΔH2TT = Δωm = 0. The contours are from the full analysis of just the WMAP data and are thus more restrictive. Right: The constraints in the ωb-ωc plane from the peak ratios in a flat geometry with ns = 0.99. The darker shaded regions in each swath are the 1σ allowed range; the lighter shaded regions show the 2σ range. The horizontal swath is for H2TT = 0.426 ± 0.015, and the vertical one is for H3TT = 0.42 ± 0.08. The leftmost vertical line is for H2TE = 0.33 ± 0.10. The uncertainty band for H2TE is not shown as it is broader than the H3TT swath. The heavier central lines correspond to ΔH2TT = 0, ΔH3TT = 0, and ΔH2TE = 0, each with Δns = 0. As the mission progresses, all uncertainties will shrink.	PNG (28 kb - 2048x1191 pixels) PNG (72 kb - 4096x2382 pixels) EPS (31 kb)